题目内容
已知四棱锥P-ABCD的三视图和直观图如下:

(1)求四棱锥P-ABCD的体积;
(2) 若E是侧棱PC上的动点,是否不论点E在何位置,都有BD⊥AE?证明你的结论.
(3) 若F是侧棱PA上的动点,证明:不论点F在何位置,都不可能有BF⊥平面PAD。
【答案】
(1)  (2)不论点E在何位置,都有BD⊥AE成立(3) 假设BF⊥平面PAD,
(2)不论点E在何位置,都有BD⊥AE成立(3) 假设BF⊥平面PAD,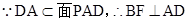


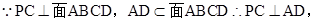

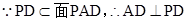 这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD
这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD
【解析】
试题分析:(1)由三视图可知,四棱锥中,PC⊥底面ABCD,底面ABCD是边长为1的正方形,PC=2,∴VP-ABCD= ·PC·S底=
·PC·S底= ×2×1=
×2×1= .
3分
.
3分
(2)不论点E在何位置,都有BD⊥AE成立. 4分
连接AC,∵BD⊥AC,BD⊥PC,且 ∴BD⊥平面PAC, 7分
∴BD⊥平面PAC, 7分
当E在PC上运动时, ,∴BD⊥AE恒成立. 8分
,∴BD⊥AE恒成立. 8分
(3)用反证法:假设BF⊥平面PAD, 9分
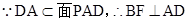
又
 11分
11分
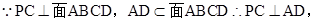
 ,
,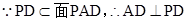 12分这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD 13分
12分这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD 13分
考点:锥体体积及线线垂直线面垂直的判定
点评:椎体体积公式 ,本题中在求解第二问第三问时还可通过空间向量的方法求解,根据已知条件可建立以点
,本题中在求解第二问第三问时还可通过空间向量的方法求解,根据已知条件可建立以点 为原点,
为原点, 为坐标轴的坐标系,通过直线的方向向量与平面的法向量判定线面位置关系
为坐标轴的坐标系,通过直线的方向向量与平面的法向量判定线面位置关系

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1. 如图,已知四棱锥P-ABCD底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.