题目内容
10.在正方体ABCD-A1B1C1D1中,E,F分别是线段C1D1,A1B1上的点且C1E=A1F=$\frac{1}{3}$A1B1,则直线BE与DF所成角的余弦值是$\frac{1}{19}$.分析 分别以边D1A1,D1C1,D1D所在直线为x,y,z轴,建立空间直角坐标系,可设正方体的边长为1,根据条件可确定B,E,D,F四点的坐标,从而得到向量$\overrightarrow{BE},\overrightarrow{DF}$的坐标,根据向量夹角余弦的坐标公式即可求出$cos<\overrightarrow{BE},\overrightarrow{DF}>$,从而得出异面直线BE,DF所成角的余弦值.
解答  解:如图,
解:如图,
以D1A1,D1C1,D1D三直线分别为x,y,z轴,建立空间直角坐标系,设正方体边长为1,则:
B(1,1,1),E($0,\frac{2}{3},0$),D(0,0,1),F(1,$\frac{1}{3}$,0);
∴$\overrightarrow{BE}=(-1,-\frac{1}{3},-1)$,$\overrightarrow{DF}=(1,\frac{1}{3},-1)$;
∴cos$<\overrightarrow{BE},\overrightarrow{DF}>$=$\frac{\overrightarrow{BE}•\overrightarrow{DF}}{|\overrightarrow{BE}||\overrightarrow{DF}|}=\frac{-\frac{1}{9}}{1+\frac{1}{9}+1}=-\frac{1}{19}$;
∴直线BE与DF所成角的余弦值是$\frac{1}{19}$.
故答案为:$\frac{1}{19}$.
点评 考查通过建立空间直角坐标系,利用空间向量解决异面直线所成角的问题的方法,能求空间点的坐标,以及由点的坐标求向量坐标,向量夹角余弦的坐标公式,弄清两异面直线所成角和这两直线的方向向量的夹角的关系.

| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{9}{13}$ | D. | $\frac{13}{9}$ |
| A. | 垂直于同一条直线的两条直线平行 | B. | 垂直于同一个平面的两条直线平行 | ||
| C. | 平行于同一个平面的两条直线平行 | D. | 平行于同一条直线的两个平面平行 |
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | (a-b)c2≥0 | C. | a2>b2 | D. | ac>bc |
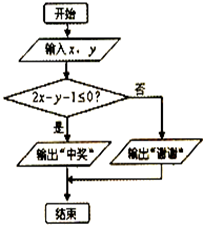 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.