题目内容
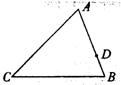 如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=
如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=| 2 |
| 3 |
A、
| ||
B、
| ||
| C、10 | ||
| D、以上答案都不对 |
分析:△ADE与△ABC相似,则存在两种情况,即△AED∽△ACB,也可能是△AED∽△ABC,应分类讨论,求解.
解答:解:如图
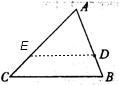
①当∠AED=∠C时,即DE∥AC
则AE=
AC=10
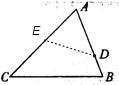
②当∠AED=∠B时,△AED∽△ABC
∴
=
,即
=
AE=
综合①②,AE=
或10
故选A.

①当∠AED=∠C时,即DE∥AC
则AE=
| 2 |
| 3 |

②当∠AED=∠B时,△AED∽△ABC
∴
| AE |
| AB |
| AD |
| AC |
| AE |
| 12 |
| 8 |
| 15 |
AE=
| 32 |
| 5 |
综合①②,AE=
| 32 |
| 5 |
故选A.
点评:此题考查了相似三角形的性质,会利用相似三角形求解一些简单的计算问题.属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
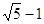 ,则AC=
,则AC= 
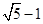 ,则AC=
,则AC= 
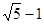 ,则AC=
,则AC=
 ,则AC=
.
,则AC=
.