Question

如图,在△ABC中,AB＝AC,∠C＝72⁰,⊙O过A、B两点且与BC相切于点B,与AC交于点D,连结BD,若BC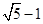＝,则AC＝         

 

Answer 1

【答案】

2

【解析】

试题分析：根据所给的三角形的两条边长相等和所给的角度，得到图形中有三个等腰三角形，根据三角形相似，得到对应边成比例得到关于所求的边的关系式，利用方程思想得到结果．解：∵AB=AC，∠C=72°，∴∠A=36°，圆O过AB两点且BC切于B，∴∠CBD=∠A=36°，∴∠ABD=36°，∴AD="BD" ，∠BDC="72°" ，BC=BD ，∴△ABC∽△BCD∴BC ²=CD?AC=（AC-BC）AC   ∴AC=2，故答案为：2

考点：圆的切线的性质，三角形相似

点评：本题考查圆的切线的性质和三角形相似的判断和性质，本题解题的关键是把所求的边表示出来再利用边之间的关系整理出来，本题是一个基础题．