题目内容
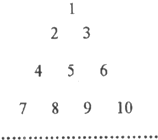 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为63
63
,56
56
.分析:第一行有一个数,第二行有两个数…,第n行有n个数字,这样每一行的数字个数组成一个等差数列,表示出等差数列的前项和,使得和大于或等于2009,解出不等式,求出n的值,在满足条件的数字附近检验,得到结果.
解答:解:由题意可知,第一行有一个数,第二行有两个数,第三行有三个数,…,第62行有62个数,第63行有63个数,第n行有n个数字,这样每一行的数字个数组成一个等差数列,
∴前n项的和是
∴
≥2009,
∵当n=63时,
=2016>2009,n≥62时,
<2009
∴第62行的最后一个数为1+2+3+…+62=1953,第63行第一个数为1954
∴2009为第63行,第56个数
即a63,56=(1+2+3+…+62)+56=
(1+62)+56=2009.
故答案为:63;56
∴前n项的和是
| n(n+1) |
| 2 |
∴
| n(n+1) |
| 2 |
∵当n=63时,
| 63(63+1) |
| 2 |
| n(n+1) |
| 2 |
∴第62行的最后一个数为1+2+3+…+62=1953,第63行第一个数为1954
∴2009为第63行,第56个数
即a63,56=(1+2+3+…+62)+56=
| 62 |
| 2 |
故答案为:63;56
点评:本题的考点是归纳推理,主要考查数列的性质和应用,本题解题的关键是看出所形成的数列是一个等差数列,利用等差数列的前项和,使得和大于或等于2009求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: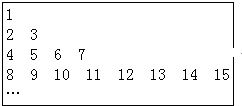 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为