题目内容
已知数列数列{an}前n项和Sn=-
n2+kn(其中k∈N*),且Sn的最大值为8.
(Ⅰ)确定常数k并求{an}的通项公式;
(Ⅱ)若bn=9-2an,求数列{
}前n项和Tn.
| 1 |
| 2 |
(Ⅰ)确定常数k并求{an}的通项公式;
(Ⅱ)若bn=9-2an,求数列{
| 1 |
| bnbn+1 |
(Ⅰ)Sn=-
n2+kn=-
(n-k)2+
k2,
又k∈N*,所以当n=k时Sn取得最大值为
k2=8,解得k=4,
则Sn=-
n2+4n,
当n≥2时,an=Sn-Sn-1=(-
n2+4n)-[-
(n-1)2+4(n-1)]=-n+
,
当n=1时,a1=-
+4=
,适合上式,
综上,an=-n+
;
(Ⅱ)由(Ⅰ)得,bn=9-2an=9-2(-n+
)=2n,
所以
=
=
(
-
),
Tn=
+
+…+
=
(1-
+
-
+…+
-
)=
(1-
)=
,
所以数列{
}前n项和Tn为
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又k∈N*,所以当n=k时Sn取得最大值为
| 1 |
| 2 |
则Sn=-
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
当n=1时,a1=-
| 1 |
| 2 |
| 7 |
| 2 |
综上,an=-n+
| 9 |
| 2 |
(Ⅱ)由(Ⅰ)得,bn=9-2an=9-2(-n+
| 9 |
| 2 |
所以
| 1 |
| bnbn+1 |
| 1 |
| 2n(2n+2) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
Tn=
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4(n+1) |
所以数列{
| 1 |
| bnbn+1 |
| n |
| 4(n+1) |

练习册系列答案
相关题目
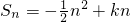 (其中k∈N*),且Sn的最大值为8.
(其中k∈N*),且Sn的最大值为8.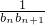 前n项和Tn.
前n项和Tn.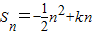 (其中k∈N*),且Sn的最大值为8.
(其中k∈N*),且Sn的最大值为8.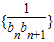 前n项和Tn.
前n项和Tn.