题目内容
已知数列数列{an}前n项和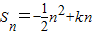 (其中k∈N*),且Sn的最大值为8.
(其中k∈N*),且Sn的最大值为8.(Ⅰ)确定常数k并求{an}的通项公式;
(Ⅱ)若bn=9-2an,求数列
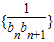 前n项和Tn.
前n项和Tn.
【答案】分析:(Ⅰ)根据二次函数的性质及k∈N*可求得Sn的最大值,令其为8,可求得k值,再根据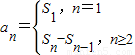 可求得an,注意验证n=1时情况;
可求得an,注意验证n=1时情况;
(Ⅱ)由(Ⅰ)易求bn,利用裂项相消法即可求得Tn.
解答:解:(Ⅰ)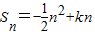 =-
=-
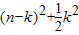 ,
,
又k∈N*,所以当n=k时Sn取得最大值为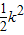 =8,解得k=4,
=8,解得k=4,
则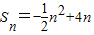 ,
,
当n≥2时,an=Sn-Sn-1=(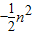 +4n)-[-
+4n)-[- (n-1)2+4(n-1)]=-n+
(n-1)2+4(n-1)]=-n+ ,
,
当n=1时,a1=- +4=
+4= ,适合上式,
,适合上式,
综上,an=-n+ ;
;
(Ⅱ)由(Ⅰ)得,bn=9-2an=9-2(-n+ )=2n,
)=2n,
所以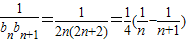 ,
,
Tn=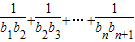 =
=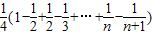 =
=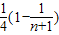 =
= ,
,
所以数列 前n项和Tn为
前n项和Tn为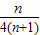 .
.
点评:本题考查等差数列的通项公式及数列求和,考查利用裂项相消法对数列求和,若{{an}为等差数列,公差为d,d≠0,则{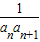 }的前n项和可用列项相消法,其中
}的前n项和可用列项相消法,其中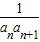 =
=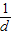 (
(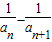 )
)
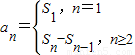 可求得an,注意验证n=1时情况;
可求得an,注意验证n=1时情况;(Ⅱ)由(Ⅰ)易求bn,利用裂项相消法即可求得Tn.
解答:解:(Ⅰ)
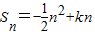 =-
=-
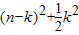 ,
,又k∈N*,所以当n=k时Sn取得最大值为
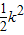 =8,解得k=4,
=8,解得k=4,则
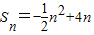 ,
,当n≥2时,an=Sn-Sn-1=(
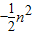 +4n)-[-
+4n)-[- (n-1)2+4(n-1)]=-n+
(n-1)2+4(n-1)]=-n+ ,
,当n=1时,a1=-
 +4=
+4= ,适合上式,
,适合上式,综上,an=-n+
 ;
;(Ⅱ)由(Ⅰ)得,bn=9-2an=9-2(-n+
 )=2n,
)=2n,所以
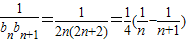 ,
,Tn=
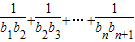 =
=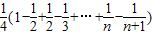 =
=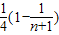 =
= ,
,所以数列
 前n项和Tn为
前n项和Tn为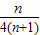 .
.点评:本题考查等差数列的通项公式及数列求和,考查利用裂项相消法对数列求和,若{{an}为等差数列,公差为d,d≠0,则{
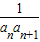 }的前n项和可用列项相消法,其中
}的前n项和可用列项相消法,其中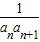 =
=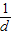 (
(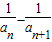 )
) 
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
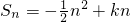 (其中k∈N*),且Sn的最大值为8.
(其中k∈N*),且Sn的最大值为8.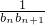 前n项和Tn.
前n项和Tn.