题目内容
“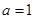 ”是“函数
”是“函数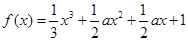 没有极值”的( )
没有极值”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析: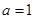 时,
时,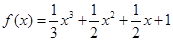 ,所以
,所以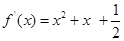 =0无实数解,即函数
=0无实数解,即函数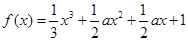 没有极值;反之,函数
没有极值;反之,函数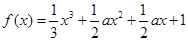 没有极值,即
没有极值,即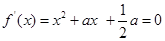 无实数解,所以
无实数解,所以 ,解得0<a<2,故“
,解得0<a<2,故“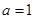 ”是“函数
”是“函数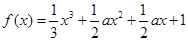 没有极值”的充分不必要条件,选A。
没有极值”的充分不必要条件,选A。
考点:本题主要考查充要条件的概念,利用导数求函数极值。
点评:基础题,充要条件的判断问题,是高考不可少的内容,特别是充要条件可以和任何知识点相结合。充要条件的判断一般有三种思路:定义法、等价关系转化法、集合关系法。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若 ,
, 是两个非零向量,则“
是两个非零向量,则“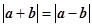 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
命题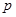 :函数
:函数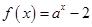 (
(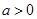 且
且 )的图像恒过点
)的图像恒过点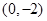 ;命题
;命题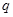 :函数
:函数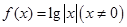 有两个零点. 则下列说法正确的是
有两个零点. 则下列说法正确的是
A.“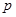 或 或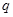 ”是真命题 ”是真命题 | B.“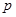 且 且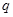 ”是真命题 ”是真命题 |
C. 为假命题 为假命题 | D.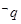 为真命题 为真命题 |
“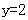 ”是“
”是“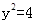 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数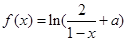 ,其中a为常数.则“
,其中a为常数.则“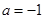 ”是f(x)为奇函数”的
”是f(x)为奇函数”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 ,使
,使 ,则( )
,则( )
A. ,使 ,使 | B. ,使 ,使 |
C. ,使 ,使 | D. ,使 ,使 |
下列命题是真命题的为
A.若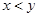 ,则 ,则 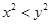 | B.若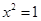 ,则 ,则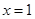 |
C.若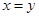 ,则 ,则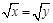 | D.若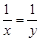 ,则 ,则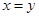 |
下列命题正确的是( )
| A.直线a与平面α不平行,则直线a与平面α内的所有直线都不平行 |
| B.如果两条直线在平面α内的射影平行,则这两条直线平行 |
| C.垂直于同一直线的两个平面平行 |
| D.直线a与平面α不垂直,则直线a与平面α内的所有直线都不垂直 |
命题“存在 ,使
,使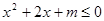 ”的否定是 ( )
”的否定是 ( )
A.存在 ,使 ,使 |
B.不存在 ,使 ,使 |
C.对于任意 ,都有 ,都有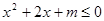 |
D.对于任意 ,都有 ,都有 |