题目内容
曲线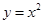 在点
在点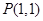 处的切线方程为( )
处的切线方程为( )
A.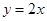 | B.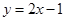 | C.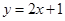 | D.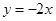 |
B
解析试题分析:求曲线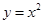 在点
在点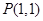 处的切线方程,首先通过对函数
处的切线方程,首先通过对函数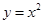 求导得
求导得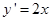 .所以所以在点
.所以所以在点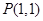 处的切线的斜率为
处的切线的斜率为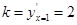 .所以切线方程为
.所以切线方程为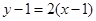 .即
.即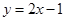 .故选B.本小题的关键是理解函数的导数的几何意义.即函数的切线的斜率.
.故选B.本小题的关键是理解函数的导数的几何意义.即函数的切线的斜率.
考点:1.函数的求导.2.用点斜式直线方程.

练习册系列答案
相关题目
函数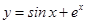 的图象上一点(0,1)处的切线的斜率为( )
的图象上一点(0,1)处的切线的斜率为( )
| A.1 | B.2 | C.3 | D.0 |
已知函数 是R上的可导函数,当
是R上的可导函数,当 时,有
时,有 ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
对于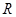 上可导的任意函数
上可导的任意函数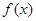 ,若满足
,若满足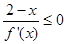 ,则必有( )
,则必有( )
A. | B.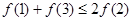 |
C.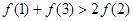 | D. |
以初速度40m/s竖直向上抛一物体,t秒时刻的速度v=40-10t2,则此物体达到最高时的高度为( ).
A.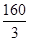 m m | B.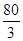 m m | C.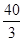 m m | D.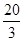 m m |
若曲线 在点
在点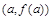 处的切线与两条坐标轴围成的三角形的面积为18,则
处的切线与两条坐标轴围成的三角形的面积为18,则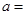 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
设函数f(x)满足x2f′(x)+2xf(x)=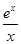 ,f(2)=
,f(2)=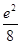 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
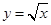 与
与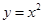 所构成(阴影部分)的区域,在D中任取一点,则该点在E中的概率是( )
所构成(阴影部分)的区域,在D中任取一点,则该点在E中的概率是( )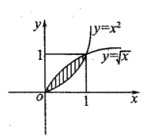
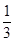
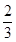
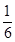
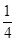
 的导函数图象如图所示,若
的导函数图象如图所示,若 为锐角三角形,则一定成立的是( )
为锐角三角形,则一定成立的是( )



