题目内容
(本小题满分12分)已知函数f(x)=lg(x2 + a x + 1)的定义域为R ,在此条件下,解关于x的不等式 x2-2x + a(2-a)< 0 .
解:由f(x)=lg(x2 + a x + 1)的定义域为R得:△=a2-4<0, ……………2分
解得:-2<a<2 ………………………… 4分
原不等式可化为:(x-a)[x - (2-a)]< 0 ………………………… 5分
(1) 当-2<a<1时,解得:a<x<2-a ;
(2) 当a=1时,不等式化为 (x-1)2 <0, 此时无解;
(3) 当1<a<2时,解得:2-a<x<a ; ………… …………… 10分
…………… 10分
综上所述:当-2<a<1时,解集为:{ x ︱a<x<2-a };
当a=1时, 解集为: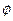
当1<a<2时,解集为:{ x ︱2-a<x<a } ………………… 12分
解得:-2<a<2 ………………………… 4分
原不等式可化为:(x-a)[x - (2-a)]< 0 ………………………… 5分
(1) 当-2<a<1时,解得:a<x<2-a ;
(2) 当a=1时,不等式化为 (x-1)2 <0, 此时无解;
(3) 当1<a<2时,解得:2-a<x<a ; …………
 …………… 10分
…………… 10分综上所述:当-2<a<1时,解集为:{ x ︱a<x<2-a };
当a=1时, 解集为:
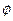
当1<a<2时,解集为:{ x ︱2-a<x<a } ………………… 12分
略

练习册系列答案
相关题目
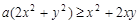 对任意非零实数
对任意非零实数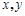 恒成立,则实数
恒成立,则实数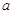 的最小值
的最小值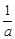 )>0的解集是
)>0的解集是 满分12分)
满分12分)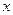 的不等式
的不等式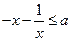 在区间
在区间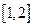 上有解,求
上有解,求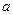 的取值范围.
的取值范围.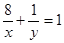 ,则
,则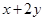 的最小值是
的最小值是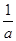 <
<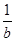 ; ②
; ②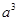 >
>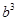 ;
;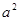 +1)>lg(b2+1); ④
+1)>lg(b2+1); ④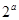 >
>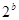
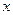 的不等式:
的不等式: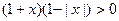 ; ②
; ②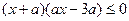 .
.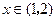 时,不等式
时,不等式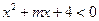 恒成立,则
恒成立,则 的值范围是 .(用区间表示)
的值范围是 .(用区间表示)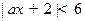 的解集是(-1,2),则实数
的解集是(-1,2),则实数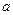 的值为
的值为