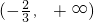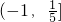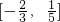题目内容
已知定义在区间[-3,3]上的函数y=f(x)满足f(-x)+f(x)=0,对于函数y=f(x)的图象上任意两点(x1,f(x1)),(x2,f(x2))都有(x1-x2)•[f(x1)-f(x2)]<0.若实数a,b满足f(a2-2a)+f(2b-b2)≤0,则点(a,b)所在区域的面积为( )
| A、8 | B、4 | C、2 | D、1 |
分析:根据条件确定函数的奇偶性和单调性,将不等式进行转化,然后利用线性规划的知识作出不等式组对应的平面区域,即可得到结论.
解答:解:∵函数y=f(x)满足f(-x)+f(x)=0,
∴f(-x)=-f(x),即函数f(x)是奇函数.
由(x1-x2)•[f(x1)-f(x2)]<0,
则函数f(x)在区间[-3,3]上是减函数.
则不等式f(a2-2a)+f(2b-b2)≤0等价为f(a2-2a)≤-f(2b-b2)=f(-2b+b2),
即
,
∴
,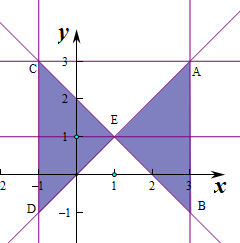
作出不等式组对应的平面区域如图:
则A(3,3),B(3,-1),E(1,1),
则对应区域的面积为2×
×4×2=8,
故选:A.
∴f(-x)=-f(x),即函数f(x)是奇函数.
由(x1-x2)•[f(x1)-f(x2)]<0,
则函数f(x)在区间[-3,3]上是减函数.
则不等式f(a2-2a)+f(2b-b2)≤0等价为f(a2-2a)≤-f(2b-b2)=f(-2b+b2),
即
|
∴
|

作出不等式组对应的平面区域如图:
则A(3,3),B(3,-1),E(1,1),
则对应区域的面积为2×
| 1 |
| 2 |
故选:A.
点评:本题主要考查函数奇偶性和单调性的应用,以及不等式的转化,利用条件将不等式转化为二元一次不等式组是解决本题的关键,综合性较强.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目