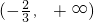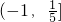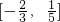Question

已知定义在区间[-3，3]上的减函数y=f（x）满足f（-x）+f（x）=0．若实数a，b满足f（a²-2a）+f（2b-b²）≤0，则点（a，b）所在区域的面积为（　　）

• A、8
• B、4
• C、2
• D、1

Answer 1

分析：由题意可得 f（a²-2a）≤-f（2b-b²）=f（b²-2b），

-3≤a2-2a≤3 -3≤b2-2b≤3 a2-2a≥b2-2b

，画出点（a b）所在的区域，如图阴影部分所示，可得此区域的面积．

解答：解：由题意可得 f（a²-2a）≤-f（2b-b²）=f（b²-2b），
∴

-3≤a2-2a≤3 -3≤b2-2b≤3 a2-2a≥b2-2b

，即

-1≤a≤3 -1≤b≤3 (a-b)(a+b-2)≥0

．
画出点（a b）所在的区域，如图阴影部分所示：
故阴影部分的面积等于正方形BCED的面积的一半，
等于

4×4

2

=8，
故选：A．

点评：本题主要考查函数的奇偶性、单调性的应用，不等式组表示平面区域，属于中档题．