题目内容
定义在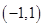 上的函数
上的函数 是奇函数,并且在
是奇函数,并且在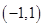 上
上 是减函数,求满足条件
是减函数,求满足条件 的
的 取值范围.( )
取值范围.( )
A. | B. | C. | D. |
A
解析试题分析:因为,定义在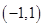 上的函数
上的函数 是奇函数,并且在
是奇函数,并且在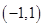 上
上 是减函数,所以,
是减函数,所以, ,
, 可化为
可化为 ,
,
故有 ,解得,
,解得, ,故选A。
,故选A。
考点:函数的奇偶性、单调性,简单不等式组的解法。
点评:中档题,涉及抽象不等式解法问题,往往利用函数的奇偶性、单调性,将抽象问题转化成具体不等式组求解,要注意函数的定义域。

练习册系列答案
相关题目
定义在 上的奇函数
上的奇函数 ,满足
,满足 ,
, ,则函数
,则函数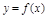 在区间
在区间 内零点个数的情况为( )
内零点个数的情况为( )
A. 个 个 | B. 个 个 | C. 个 个 | D.至少 个 个 |
设 是定义在实数集
是定义在实数集 上的函数,满足条件
上的函数,满足条件 是偶函数,且当
是偶函数,且当 时,
时, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )
A. |
B. |
C.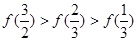 |
D. |
函数 .满足
.满足 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
下列函数中,最小值为4的函数是( )
A. | B. |
C. | D. |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )



 满足
满足 ,且在[-1,0]上单调递增,设
,且在[-1,0]上单调递增,设 ,
,  ,
, ,则
,则 大小关系是( )
大小关系是( )




