题目内容
在以下关于向量的命题中，不正确的是（ ）
A、若向量
| ||||||||
B、在△ABC中，
| ||||||||
C、四边形ABCD是菱形的充要条件是
| ||||||||
D、点G是△ABC的重心，则
|
分析：根据向量数量积判断两个向量的垂直关系的方法，我们可以判断A的真假；根据向量夹角的定义，我们可以判断B的真假；根据菱形的定义及相等向量及向量的模的概念，我们可以判断C的真假；根据三角形重心的性质，可判断D的真假，进而得到答案．
解答：解：若向量
=（x，y），向量
=（-y，x），则
•
=0，则
⊥
，故A正确；
在△ABC中，
和
的夹角等于角A的补角，故B错误；
由菱形是邻边相等的平行四边形，故四边形ABCD是菱形的充要条件是
=
，且|
|=|
|，故C正确；
由重心的性质，易得
+
+
=
?G是△ABC的重心，故D正确；
故选B
| a |
| b |
| a |
| b |
| a |
| b |
在△ABC中，
| AB |
| CA |
由菱形是邻边相等的平行四边形，故四边形ABCD是菱形的充要条件是
| AB |
| DC |
| AB |
| AD |
由重心的性质，易得
| GA |
| GB |
| GC |
| 0 |
故选B
点评：本题考查的知识点是向量的夹角，数量积判断两个向量的垂直关系，相等向量与向量的模，是对向量基本概念和基本方法的直接考查，属于基础题型，难度不大，熟练掌握相关概念和方法即可解答．D中应该G是△ABC的重心，则
+
+
=
！！
| GA |
| GB |
| GC |
| 0 |
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
在以下关于向量的命题中，不正确的是（ ）
| A、若向量a=（x，y），向量b=（-y，x），（xy≠0），则a⊥b | ||||||||
B、平行四边形ABCD是菱形的充要条件是（
| ||||||||
C、点G是△ABC的重心，则
| ||||||||
D、△ABC中，
|
在以下关于向量的命题中，不正确的是（ ）
A、若向量
| ||||||||
B、△ABC中，有
| ||||||||
C、△ABC中
| ||||||||
D、已知四边形ABCD，则四边形ABCD是菱形的充要条件是
|
.
+
+
=
和
的夹角等于180°－A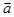
=（x, y），向量
=(－y,x) (xy≠0)，则
的夹角为角A