题目内容
在以下关于向量的命题中，不正确的是（ ）
A、若向量
| ||||||||
B、△ABC中，有
| ||||||||
C、△ABC中
| ||||||||
D、已知四边形ABCD，则四边形ABCD是菱形的充要条件是
|
分析：（A）利用数量积是否为0来判断是否垂直．
（B）利用向量加法的三角形法则可知为正确．
（C）研究向量夹角要保证向量起点相同．
（D）将向量形式转化成四边形ABCD边的位置关系和数量关系去判断．
（B）利用向量加法的三角形法则可知为正确．
（C）研究向量夹角要保证向量起点相同．
（D）将向量形式转化成四边形ABCD边的位置关系和数量关系去判断．
解答：解：（A）
•
=1×（-2）+2×1=0，∴
⊥
A对
（B）利用向量加法的三角形法则可知为正确．
（C）如图，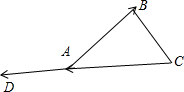
将向量
平移至
，则∠BAD为
和
的夹角．与A是互补关系．（C）错
（D）
=
，说明AB 与CD平行且相等．所以ABCD是平行四边形；又|
|=|
|，说明邻边AB，CD相等，∴四边形ABCD是菱形，反之也成立．D对
故选C．
| a |
| b |
| a |
| b |
（B）利用向量加法的三角形法则可知为正确．
（C）如图，
将向量| CA |
| AD |
| AB |
| CA |
（D）
| AB |
| DC |
| AB |
| AD |
故选C．
点评：本题考查向量的基本知识及应用，向量夹角的概念、向量的运算．属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
在以下关于向量的命题中，不正确的是（ ）
| A、若向量a=（x，y），向量b=（-y，x），（xy≠0），则a⊥b | ||||||||
B、平行四边形ABCD是菱形的充要条件是（
| ||||||||
C、点G是△ABC的重心，则
| ||||||||
D、△ABC中，
|
在以下关于向量的命题中，不正确的是（ ）
A、若向量
| ||||||||
B、在△ABC中，
| ||||||||
C、四边形ABCD是菱形的充要条件是
| ||||||||
D、点G是△ABC的重心，则
|
.
+
+
=
和
的夹角等于180°－A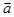
=（x, y），向量
=(－y,x) (xy≠0)，则
的夹角为角A