题目内容

若双曲线的焦点为F1（-4，0），F2（4，0），实轴长与虚轴长相等，则双曲线的标准方程为：______．
由于实轴长与虚轴长相等，
则可设等轴双曲线方程为x2-y2=a（a＞0），
化成标准方程：
x2
a
-
y2
a
=1
由标准方程得：c=
2
a
=4，
∴a=8
∴所求的等轴双曲线方程为
x2
8
-
y2
8
=1，
故答案为：
x2
8
-
y2
8
=1．
练习册系列答案
相关题目
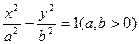双曲线的左、右焦点分别为F1，F2，点P为该双曲线在第一象限的点，△PF1F2面积为1，且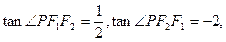则该双曲线的方程为
A．B．
C．D．
（1）点M到点F（2，0）的距离比它到直线x=-3的距离小1，求点M满足的方程．
（2）曲线上点M（x，y）到定点F（2，0）的距离和它到定直线x=8的距离比是常数2，求曲线方程．
已知双曲线的一个焦点与抛物线x2=20y的焦点重合，且其渐近线的方程为3x±4y=0，则该双曲线的标准方程为（　　）
A．
x2
9
-
y2
16
=1		B．
x2
16
-
y2
9
=1		C．
y2
9
-
x2
16
=1		D．
y2
16
-
x2
9
=1
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的离心率为
3
，右准线方程为x=
3
3
．
（Ⅰ）求双曲线C的方程；
（Ⅱ）已知直线x-y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值．
双曲线
y2
9
-
x2
16
=1上的一点P到它一个焦点的距离为4，则点P到另一焦点的距离是（　　）
A．2B．10C．10或2D．14
设双曲线C：
x2
a2
-
y2
b2
=1（a，b＞0）的一条渐近线与抛物线x=y2的一个交点的横坐标为x0，若x0＞
1
2
，则双曲线C的离心率的取值范围是（　　）
A．(1，
6
2
)		B．(1，
3
)		C．(
3
，+∞)		D．(
6
2
，+∞)
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点为F，过F且斜率为
3
的直线交C于A、B两点，若
AF
=4
FB
，则双曲线C的离心率为______．
曲线
x2
25
-
y2
9
=1与曲线
x2
25-k
-
y2
9+k
=1(-9＜k＜25)的（　　）
A．实轴长相等B．虚轴长相等C．离心率相等D．焦距相等

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网