题目内容
(本小题14分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;
(2)现有两个奖励函数模型:(1)y=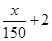 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
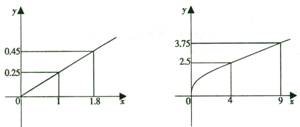
(1)当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③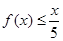 恒成立
恒成立
(2)所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-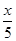 <0,即4lgx-3<
<0,即4lgx-3<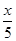 ,所以
,所以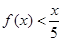 恒成立
恒成立
【解析】解:(1)设奖励函数模型为y=f(x),则公司对函数模型的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③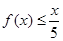 恒成立…5分
恒成立…5分
(2)①对于函数模型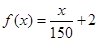 :
:
当x∈[10,1000]时,f(x)是增函数, …………………… 6分
则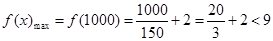 .所以f(x)≤9恒成立.… 8分
因为函数
.所以f(x)≤9恒成立.… 8分
因为函数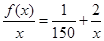 在[10,1000]上是减函数,所以
在[10,1000]上是减函数,所以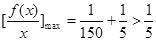 .
.
从而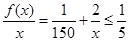 ,即
,即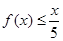 不恒成立.
不恒成立.
故该函数模型不符合公司要求. ………………………… 10分
②对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数, …………… 11分
则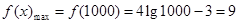 .所以f(x)≤9恒成立.……… 13分
.所以f(x)≤9恒成立.……… 13分
设g(x)=4lgx-3-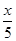 ,则
,则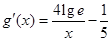 .
.
当x≥10时,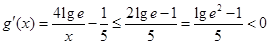 ,
,
所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-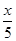 <0,即4lgx-3<
<0,即4lgx-3<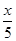 ,所以
,所以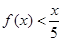 恒成立.
恒成立.
故该函数模型符合公司要求.………………………… 15分

(本小题14分)某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
|
资 金 |
单位产品所需资金(百元) |
月资金供应量(百元) |
|
|
空调机 |
洗衣机 |
||
|
成 本 |
30 |
20 |
300 |
|
劳动力(工资) |
5 |
10 |
110 |
|
单位利润 |
6 |
8 |
|
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
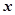 (万元)的函数关系式;
(万元)的函数关系式;