题目内容
12、若直线ax+y+1=0与连接A(2,3),B(-3,2)两点的线段AB相交,则实数a的取值范围是
a≤-2或a≥1
.分析:由直线ax+y+1=0的方程,判断恒过P(0,-1),求出KPA与KPB,判断过P点的竖直直线与AB两点的关系,求出满足条件的直线斜率的取值范围.
解答:解:由直线ax+y+1=0的方程,判断恒过P(0,-1),
如下图示:
∵KPA=2,KPB=-1,
则实数a的取值范围是:a≤-2或a≥1.
故答案为:a≤-2或a≥1.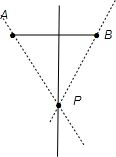
如下图示:
∵KPA=2,KPB=-1,
则实数a的取值范围是:a≤-2或a≥1.
故答案为:a≤-2或a≥1.

点评:求恒过P点且与线段AB相交的直线的斜率的取值范围,有两种情况:
当AB,在P竖直方向上的同侧时,(如本题)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈[KPA,KPB]
当AB,在P竖直方向上的异侧时,(如下图)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈(-∞,KPA]∪[KPB,+∞)
就是过p点的垂直x轴的直线与线段有交点时,斜率范围写两段区间,无交点时写一段区间.
当AB,在P竖直方向上的同侧时,(如本题)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈[KPA,KPB]
当AB,在P竖直方向上的异侧时,(如下图)计算KPA与KPB,若KPA<KPB,则直线的斜率k∈(-∞,KPA]∪[KPB,+∞)
就是过p点的垂直x轴的直线与线段有交点时,斜率范围写两段区间,无交点时写一段区间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目