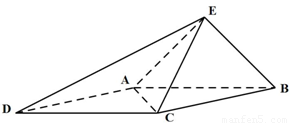
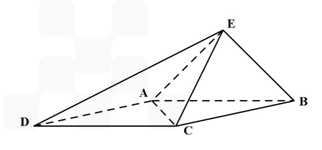
题目内容
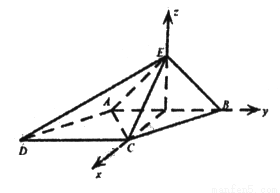
如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=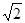
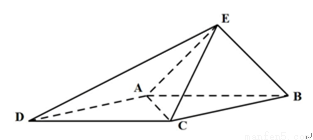
(1)求证:平面EAB⊥平面ABCD
(2)求二面角A-EC-D的余弦值
【答案】
(1)先证EO⊥平面ABCD即可得证 (2)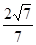
【解析】
试题分析:(1)证明:取AB的中点O,连接EO,CO
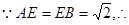 △AEB为等腰直角三角形
△AEB为等腰直角三角形
∴EO⊥AB,EO=1
又∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,
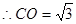 ,又
,又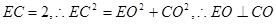
∵EO⊥平面ABCD,又EO 平面EAB,∴平面EAB⊥平面ABCD
平面EAB,∴平面EAB⊥平面ABCD
(2)以AB的中点O为坐标原点,OB所在直线为y轴,OE所在直线为z轴,如图建系则
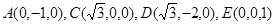 ,
,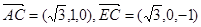 ,
,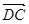 =
=
(0,2,0)
设平面DCE的法向量为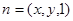 ,则
,则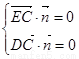 ,即
,即 ,解得:
,解得:
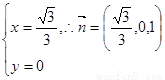
同理求得平面EAC的一个法向量为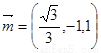
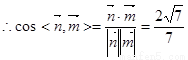 ,所以二面角A-EC-D的余弦值为
,所以二面角A-EC-D的余弦值为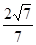
考点:用空间向量求平面间的夹角 平面与平面垂直判定 二面角的平面角及求法
点评:本题给出特殊四棱锥,求证面面垂直并求二面角的余弦值,着重考查了空间线面垂直、
面面垂直的判定与性质和利用空间向量的方法求面面所成角的知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=
(2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=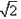 .
.
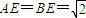 .
.