题目内容
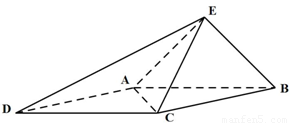
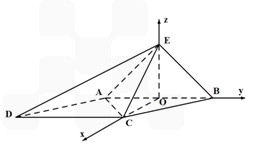
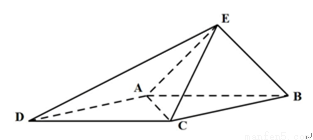
如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=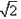 .
.
(I)求证:平面EAB⊥平面ABCD;
(II)求二面角A-EC-D的余弦值.
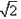 .
.(I)求证:平面EAB⊥平面ABCD;
(II)求二面角A-EC-D的余弦值.
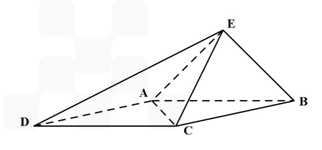
(I)证明:取AB的中点O,连接EO,CO
∵AE=EB=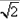 ,AB=2
,AB=2
∴△AEB为等腰直角三角形
∴EO⊥AB,EO=1
又∵AB=BC,∠ABC=60°
∴△ACB是等边三角形
∴CO=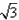 ,又EC=2
,又EC=2
∴EC2=EO2+CO2,∴EO⊥CO
∴EO⊥平面ABCD,又EO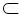 平面EAB
平面EAB
∴平面EAB⊥平面ABCD
(II)以AB中点O为坐标原点,以OB所在直线为y轴,OE所在直线为z轴,建立空间直角坐标系如图所示,则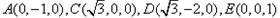
∴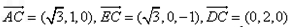
设平面DCE的法向量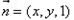
∴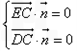 ,即
,即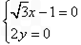 ,解得
,解得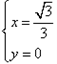 ,∴
,∴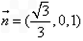
设平面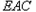 的法向量
的法向量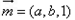
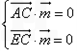 ,
,
即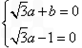 ,解得
,解得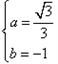
∴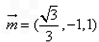 ,
,
∵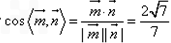
所以二面角A-EC-D的余弦值为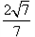

练习册系列答案
相关题目
 (2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=
(2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=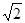
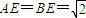 .
.