题目内容
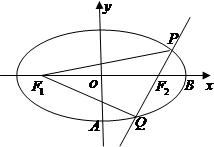
设F1、F2为椭圆的左右焦点，过椭圆| x2 |
| 25 |
| y2 |
| 16 |
| PF1 |
| PF2 |
分析：欲求四边形PF1QF2面积最大时，
•
的值，根据图形的几何性质得到该四边形是平行四边形．
此四边形可以成两个全等三角形的组合图形，SPF1QF2=|
||
| sinθ，当θ取最大值时四边形PF1QF2面积最大，易得当点P、Q分别在上下顶点时符合要求．于是
•
=|
|2cosθ，即可得到结果．
| PF1 |
| PF2 |
此四边形可以成两个全等三角形的组合图形，SPF1QF2=|
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| PF1 |
解答：解：因为四边形是平行四边形，
所以，四边形可以成两个全等三角形的组合图形，则SPF1QF2=|
||
| sinθ；
当θ取最大值时四边形PF1QF2面积最大，sinθ=
即当点P、Q分别在上下顶点时，θ取最大值，四边形PF1QF2面积最大，
令椭圆的实半轴为a=5，虚半轴为b=4，焦半径为c
此时，
•
=|
|2cosα=a2
=25×
=7．
故答案为7．
所以，四边形可以成两个全等三角形的组合图形，则SPF1QF2=|
| PF1 |
| PF2 |
当θ取最大值时四边形PF1QF2面积最大，sinθ=
| 24 |
| 25 |
即当点P、Q分别在上下顶点时，θ取最大值，四边形PF1QF2面积最大，
令椭圆的实半轴为a=5，虚半轴为b=4，焦半径为c
此时，
| PF1 |
| PF2 |
| PF1 |
1-(
|
| 7 |
| 25 |
故答案为7．
点评：本题考查平面向量数量积的运算，同时还考查与椭圆相关的知识．
练习册系列答案
阅读快车系列答案
相关题目
已知椭圆