题目内容
下列判断正确的是
①函数y=|x-1|与y=
是同一函数;
②若函数f(x)在区间(-∞,0)上递增,在区间[0,+∞)上也递增,则函数f(x)必在R上递增;
③对定义在R上的函数f(x),若f(2)≠f(-2),则函数f(x)必不是偶函数;
④函数f(x)=
在(-∞,0)∪(0,+∞)上单调递减;
⑤若x1是函数f(x)的零点,且m<x1<n,那么f(m)•f(n)<0.
③
③
(把正确的序号都填上).①函数y=|x-1|与y=
|
②若函数f(x)在区间(-∞,0)上递增,在区间[0,+∞)上也递增,则函数f(x)必在R上递增;
③对定义在R上的函数f(x),若f(2)≠f(-2),则函数f(x)必不是偶函数;
④函数f(x)=
| 1 |
| x |
⑤若x1是函数f(x)的零点,且m<x1<n,那么f(m)•f(n)<0.
分析:①函数y=|x-1|=
与y=
的定义域不同;
②例如函数y=
可以说明②错误
③由偶函数的定义可知,若f(x)为偶函数,则对任意的f(-x)=f(x);
④函数f(x)=
在(-∞,0),(0,+∞)上单调递减,不能用“∪”连接单调区间
⑤只有x1为区间(m,n)内唯一的零点时,才有f(m)•f(n)<0
|
|
②例如函数y=
|
③由偶函数的定义可知,若f(x)为偶函数,则对任意的f(-x)=f(x);
④函数f(x)=
| 1 |
| x |
⑤只有x1为区间(m,n)内唯一的零点时,才有f(m)•f(n)<0
解答:解:①函数y=|x-1|=
与y=
的定义域不同,故不是同一函数;①错误
②例如函数y=
在区间(-∞,0)上递增,在区间[0,+∞)上也递增,函数f(x)在R上不是递增;②错误
③由偶函数的定义可知,若f(x)为偶函数,则对任意的f(-x)=f(x),从而可得,f(2)≠f(-2),则函数f(x)必不是偶函数;③正确
④函数f(x)=
在(-∞,0),(0,+∞)上单调递减,不能用“∪”连接单调区间;④错误
⑤若x1是函数f(x)的零点,且m<x1<n,且x1为区间(m,n)内唯一的零点时,才有f(m)•f(n)<0.⑤错误
故答案为:③
|
|
②例如函数y=
|
③由偶函数的定义可知,若f(x)为偶函数,则对任意的f(-x)=f(x),从而可得,f(2)≠f(-2),则函数f(x)必不是偶函数;③正确
④函数f(x)=
| 1 |
| x |
⑤若x1是函数f(x)的零点,且m<x1<n,且x1为区间(m,n)内唯一的零点时,才有f(m)•f(n)<0.⑤错误
故答案为:③
点评:本题主要考察了函数知识的综合应用,解题的关键是熟练掌握函数的基本知识并能灵活应用.

练习册系列答案
相关题目
已知函数y=sin(x-
)cos(x-
),则下列判断正确的是( )
| π |
| 12 |
| π |
| 12 |
A、此函数的最小正周期为2π,其图象的一个对称中心是(
| ||
B、此函数的最小正周期为π,其图象的一个对称中心是(
| ||
C、此函数的最小正周期为2π,其图象的一个对称中心是(
| ||
D、此函数的最小正周期为π,其图象的一个对称中心是(
|
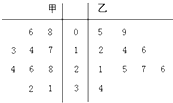 6、在如图所示的茎叶图中,若甲、乙两组数据的中位数分别为λ1,λ2,平均数分别为μ1,μ2,则下列判断正确的是( )
6、在如图所示的茎叶图中,若甲、乙两组数据的中位数分别为λ1,λ2,平均数分别为μ1,μ2,则下列判断正确的是( ) (2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
(2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中