题目内容
已知等差数列{an}的前n项和为Sn，若(a2－1)3＋2 012·(a2－1)＝1，(a2 011－1)3＋2 012(a2 011－1)＝－1，则下列四个命题中真命题的序号为________．
①S2 011＝2 011；②S2 012＝2 012；③a2 011＜a2；④S2 011＜S2.
②③
【解析】该题通过条件(a2－1)3＋2 012(a2－1)＝1，(a2 011－1)3＋2 012(a2 011－1)＝－1，考查函数与方程的思想，由于函数f(x)＝x3＋x是奇函数，由条件有f(a2－1)＝1，f(a2 011－1)＝－1.另外，f′(x)＝3x2＋1＞0，所以，f(x)是单调递增的，而f(1)＝2＞1＝f(a2－1)，∴a2－1＜1，a2＜2，所以，a2－1＝－(a2 011－1)，∴a2＋a2 011＝2，且a2－1＞a2 011－1，∴a2＞0＞a2 011；又由等差数列{an}考查等差数列概念与通项公式，由此可得S2 012＝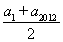
×2 012＝2 012，d＜0，∴S2 011＝S2 012－a2 012＝2 012－(2－a2＋d)＝2 010＋a1＞a1＋a2＝S2.
练习册系列答案
相关题目
