Question

（本小题满分12分）
已知向量a=(2,1),b=(x,y).
（1） 若x∈{-1,0,1,2}，y∈{-1,0,1}，求向量a∥b的概率；
（2） 若x∈［-1,2］，y∈［-1,1］，求向量a,b的夹角是钝角的概率.

Answer 1

解：（1） 设“a∥b”为事件A，由a∥b，得x=2y.

Ω={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),(2,-1),(2,0),(2,1)}
共包含12个基本事件；……………………………………………… 3分
其中A={（0，0），（2，1）}，包含2个基本事件.
则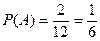.………………………………………………… 6分
（2） 设“a，b的夹角是钝角”为事件B，由a，b的夹角是钝角，可得a·b＜0,即2x+y＜0,且x≠2y.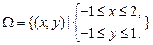

第18题答案图

则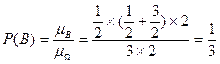.………………………………12分

解析