题目内容
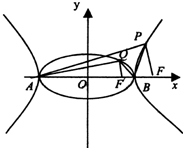 如图,F′,F分别为椭圆
如图,F′,F分别为椭圆| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| PB |
| QA |
| QB |
| PF |
| 3 |
| QF′ |
(1)求出椭圆和双曲线的离心率;
(2)设直线PA、PB、QA、QB的斜率分别是k1,k2,k3,k4,求证:k1+k2+k3+k4=0.
分析:(1)设O为原点,由向量条件得
=λ
,于是O、P、Q三点共线,因为
=
所以PF∥QF′,且 |PF|=
|QF′|得λ=
=
=
=
,代入a,b化简即得a,b的关系式,从而得出椭圆和双曲线的离心率;
( 2)设P(x1,y1)、Q(x2,y2),利用斜率公式得到:k1+k2=
+
=
=
;同理可得k3+k4=-
结合O、P、Q三点共线即可得出k1+k2+k3+k4的值.
| PO |
| QO |
| PF |
| 3 |
| QF′ |
| 3 |
| |OP| |
| |OQ| |
| |PF| |
| |QF′| |
| |OF| |
| |OF′| |
| 3 |
( 2)设P(x1,y1)、Q(x2,y2),利用斜率公式得到:k1+k2=
| y1 |
| x1+a |
| y1 |
| x1-a |
| 2x1y1 | ||
|
| x1 |
| y1 |
| x2 |
| y2 |
解答:解:(1)设O为原点,则
+
=2
,
+
=2
.
而
+
=λ(
+
),得
=λ
,
于是O、P、Q三点共线. (2分)
因为
=
所以PF∥QF′,且 |PF|=
|QF′|,(3分)
得λ=
=
=
=
,
∴
=3,
∴a2=2b2(5分)
因此椭圆的离心率为
.双曲线的离心率为
.(7分)
( 2)设P(x1,y1)、Q(x2,y2),
点P在双曲线
-
=1的上,有
-
=1.
则x12-2b2=2y12.
所以k1+k2=
+
=
=
. ①(9分)
又由点Q在椭圆
+
=1上,有x22-2b2=-2y22.
同理可得k3+k4=-
②(10分)
∵O、P、Q三点共线.
∴
=
.
由①、②得k1+k2+k3+k4=0. (12分)
| PA |
| PB |
| PO |
| QA |
| QB |
| QO |
而
| PA |
| PB |
| QA |
| QB |
| PO |
| QO |
于是O、P、Q三点共线. (2分)
因为
| PF |
| 3 |
| QF′ |
| 3 |
得λ=
| |OP| |
| |OQ| |
| |PF| |
| |QF′| |
| |OF| |
| |OF′| |
| 3 |
∴
| a2+b2 |
| a2-b2 |
∴a2=2b2(5分)
因此椭圆的离心率为
| ||
| 2 |
| ||
| 2 |
( 2)设P(x1,y1)、Q(x2,y2),
点P在双曲线
| ||
| 2b2 |
| ||
| b2 |
| ||
| 2b2 |
| ||
| b2 |
则x12-2b2=2y12.
所以k1+k2=
| y1 |
| x1+a |
| y1 |
| x1-a |
| 2x1y1 | ||
|
| x1 |
| y1 |
又由点Q在椭圆
| ||
| 2b2 |
| ||
| b2 |
同理可得k3+k4=-
| x2 |
| y2 |
∵O、P、Q三点共线.
∴
| x1 |
| y1 |
| x2 |
| y2 |
由①、②得k1+k2+k3+k4=0. (12分)
点评:本小题主要考查椭圆的几何性质、双曲线的几何、圆锥曲线的综合等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
相关题目
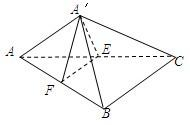 如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C.
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C.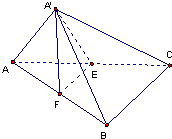 如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,使A′C=
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,使A′C= 如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C,P为A′C的中点.
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C,P为A′C的中点. 如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是
如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是