题目内容
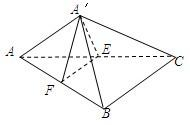 如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C.
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C.(Ⅰ)求证:平面A′EC⊥平面A′BC;
(Ⅱ)求证:AA′⊥平面A′BC;
(Ⅲ)过EF作一平面EFPQ同时与直线AA′、BC平行设交A′B、A′C分别于P、Q两点,试指出P、Q的位置,并求截面EFPQ分四面体A′ABC的两部分的体积比:VA'AEFPQ:VPQEFBC.
分析:(Ⅰ)要证平面A′EC⊥平面A′BC,只需证明平面A′BC内的直线BC垂直平面A′EC内的两条相交直线A′E、AC即可证明BC⊥平面A′EC;
(Ⅱ)要证AA′⊥平面A′BC,只需证明直线AA′垂直平面A′BC内的两条相交直线BC、A′C即可;
(Ⅲ)取AB、A′C的中点P、Q,说明平面EFPQ同时与AA′、BC平行,分别求出截面EFPQ分四面体A′ABC的两部分的体积比:VA'AEFPQ:VPQEFBC.
(Ⅱ)要证AA′⊥平面A′BC,只需证明直线AA′垂直平面A′BC内的两条相交直线BC、A′C即可;
(Ⅲ)取AB、A′C的中点P、Q,说明平面EFPQ同时与AA′、BC平行,分别求出截面EFPQ分四面体A′ABC的两部分的体积比:VA'AEFPQ:VPQEFBC.
解答: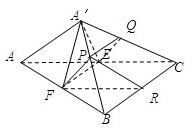 解:(Ⅰ)∵AC是直角△ABC的直角边E、F分别是AC、AB中点
解:(Ⅰ)∵AC是直角△ABC的直角边E、F分别是AC、AB中点
∴EF∥BC∵BC⊥AC∴EF⊥AC∵EF⊥A′E
∴BC⊥A′E∵A′E∩AC=E
A′E、AC?平面A'EC
∴BC⊥平面A′EC又∵BC?平面A′BC
∴平面A′EC⊥平面A′BC (5分);
(Ⅱ)∵BC⊥平面A′ECAA′?平面A′
EC∴BC⊥AA′
又∵EA=EC=EA′∴∠AA′C=90°
∴AA′⊥C∵BC∩A′C=C,BC、A′C?平面A′BC
∴AA′⊥平面A′BC10′
(Ⅲ)取AB、A′C的中点P、Q,∴PQ=∥
BC,∵EF=∥
BC
∴EF=∥PQ∴E、F、P、Q四点共面,易知平面EFPQ
同时与AA′、BC平行.取BC的中点R连PR、FR
设S△BRF=S,P到平面ABC的距离为h,
∴VBFEQC=
Sh+Sh=
ShVA′-ABC=
∴VA'AEFPQ:VPQEFBC=1:1. (15分)
 解:(Ⅰ)∵AC是直角△ABC的直角边E、F分别是AC、AB中点
解:(Ⅰ)∵AC是直角△ABC的直角边E、F分别是AC、AB中点∴EF∥BC∵BC⊥AC∴EF⊥AC∵EF⊥A′E
∴BC⊥A′E∵A′E∩AC=E
A′E、AC?平面A'EC
∴BC⊥平面A′EC又∵BC?平面A′BC
∴平面A′EC⊥平面A′BC (5分);
(Ⅱ)∵BC⊥平面A′ECAA′?平面A′
EC∴BC⊥AA′
又∵EA=EC=EA′∴∠AA′C=90°
∴AA′⊥C∵BC∩A′C=C,BC、A′C?平面A′BC
∴AA′⊥平面A′BC10′
(Ⅲ)取AB、A′C的中点P、Q,∴PQ=∥
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=∥PQ∴E、F、P、Q四点共面,易知平面EFPQ
同时与AA′、BC平行.取BC的中点R连PR、FR
设S△BRF=S,P到平面ABC的距离为h,
∴VBFEQC=
| 1 |
| 3 |
| 4 |
| 3 |
| 8sh |
| 3 |
∴VA'AEFPQ:VPQEFBC=1:1. (15分)
点评:本题考查平面与平面垂直的判定,直线与平面垂直的判定,棱锥的体积,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
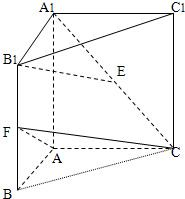 如图,直三棱柱ABC-A1B1C1中,AB=1,
如图,直三棱柱ABC-A1B1C1中,AB=1,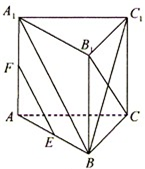 如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,BC=CC1,E、F分别为AB、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,BC=CC1,E、F分别为AB、AA1的中点. 如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为 (2006•宝山区二模)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=90°,AC1与底面成60°角,E、F分别为AA1、AB的中点.求异面直线EF与A1C所成角的大小.
(2006•宝山区二模)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=90°,AC1与底面成60°角,E、F分别为AA1、AB的中点.求异面直线EF与A1C所成角的大小.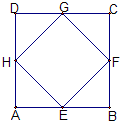 (2010•台州二模)如图,E,F,G,H分别是正方形ABCD各边的中点,将等腰 三角形EFB,FGC,GHD,HEA分别沿其底边折起,使其与原 所在平面成直二面角,则所形成的空间图形中,共有异面直线 段的对数为
(2010•台州二模)如图,E,F,G,H分别是正方形ABCD各边的中点,将等腰 三角形EFB,FGC,GHD,HEA分别沿其底边折起,使其与原 所在平面成直二面角,则所形成的空间图形中,共有异面直线 段的对数为