题目内容

给出下列命题：
①若a，b∈R⁺，a≠b则a³+b³＞a²b+ab²．
②若a，b∈R⁺，a＜b，则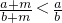 $数学公式$
③若a，b，c∈R⁺，则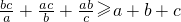 $数学公式$ ．
④若3x+y=1，则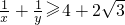 $数学公式$
其中正确命题的个数为

A.
1个
B.
2个
C.
3个
D.
4个

B
分析：利用做差比较法能够得到①为真；m的正负未知故②不能确定；利用均值不等式能够导出③为真；x，y正负未知，故④不成立．
解答：（a³+b³）-（a²b+ab²）=（a-b）²（a+b）＞0所以①为真；
m的正负未知故②不能确定；
$\text{[math]}$ + $\text{[math]}$ ≥2c， $\text{[math]}$ + $\text{[math]}$ ≥2b， $\text{[math]}$ + $\text{[math]}$ ≥2a，三式相加故③为真；
x，y正负未知，故④不成立．
故选B．
点评：本题考查基本不等式的性质和应用，解题时要注意公式的合理运用．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

给出下列命题：
①如果向量

共面，向量

也共面，则向量

共面；
②已知直线a的方向向量

与平面α，若

∥平面α，则直线a∥平面α；
③若P、M、A、B共面，则存在唯一实数x、y使

；
④对空间任意点O与不共线的三点A、B、C，若

（其中x+y+z=1），则P、A、B、C四点共面；在这四个命题中为真命题的序号有

给出下列命题：①已知

；②A，B，M，N为空间四点，若

不构成空间的一个基底，那么A，B，M，N共面；③已知

与任何向量都不构成空间的一个基底；④若

所在直线或者平行或者重合．正确的结论为

（2007•烟台三模）给出下列命题：
①存在实数a，使sinacosa=1；
②存在实数a，使sina+cosa=

π-2x）是偶函数；
④x=

是函数y=sin（2x+

π）的一条对称轴方程；
⑤若α、β是第一象限角，则tanα＞tanβ
其中正确命题的序号是

．（注：把所有正确命题的序号都填上）

用a、b、c表示不同的直线，r表示平面，给出下列命题：

(1)若a∥b，b∥c，则a∥c

(2)若a⊥b，b⊥c，则a⊥c

(3)若a∥r，b∥r，则a∥b

(4)若a⊥r，b⊥r，则a∥b

其中真命题的序号是

(1)(2)

(2)(3)

(1)(4)

(3)(4)

设a，b为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：

(1)若a∥α且b∥α，则a∥b；

(2)若a⊥α且a⊥β，则α∥β；

(3)若，则一定存在平面γ，使得；

(4)若，则一定存在直线l，使得．

上面命题中，所有真命题的序号是________．