Question

如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆．
求证：（1）AC是⊙D的切线；（2）AB+EB=AC．

Answer 1

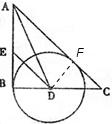
证明：（1）过点D作DF⊥AC于F；（1分）
∵AB为⊙D的切线，AD平分∠BAC，
∴BD=DF，（3分）
∴AC为⊙D的切线．（4分）
（2）在△BDE和△DCF中；
∵BD=DF，DE=DC，
∴△BDE≌△DCF，（6分）
∴EB=FC．（8分）
∵AB=AF，
∴AB+EB=AF+FC，
即AB+EB=AC．（10分）