题目内容
3、平面α∥平面β，AB、CD是夹在α和β间的两条线段，E、F分别为AB、CD的中点，则EF与α的关系是（ ）
分析：由于AB，CD的位置关系不确定，故要分AB∥CD，AB，CD相交，及AB，CD异面三种情况来讨论，其中前两种情况由面面平行的性质定理，可以将其转化为一个平面问题，易得到结论，当AB与CD异面时，可以添加辅助线将空间问题转化为平面问题，再进行判断．
解答：解：若AB∥CD，易得EF与α、β均平行
若AB与CD相交，则EF与α、β均平行
若AB与CD异面，则
设过AB和EF的平面交α，β分别于直线AG和BH，如下图所示：
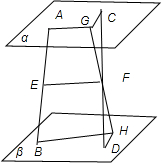
且使G，F，H在一直线上．
因为平面α∥β，所以AG∥CH，连接CG和DH，则CGFDH在一个平面内，且
CG∥DH，F为CD中点，所以三角形CFG和三角形DFH全等，即得FG=FH，
因为AG∥CH，又E，F分别为AB，CD中点，且A，C，H，G在一个平面内，所以
EF∥AG∥CH，CH在平面β内，故EF∥β．
同理EF∥β
故选A
若AB与CD相交，则EF与α、β均平行
若AB与CD异面，则
设过AB和EF的平面交α，β分别于直线AG和BH，如下图所示：
且使G，F，H在一直线上．
因为平面α∥β，所以AG∥CH，连接CG和DH，则CGFDH在一个平面内，且
CG∥DH，F为CD中点，所以三角形CFG和三角形DFH全等，即得FG=FH，
因为AG∥CH，又E，F分别为AB，CD中点，且A，C，H，G在一个平面内，所以
EF∥AG∥CH，CH在平面β内，故EF∥β．
同理EF∥β
故选A
点评：本题考查的知识点是空间中直线与平面之间的位置关系，由于AB，CD的位置关系不确定，故要进行分类讨论，另外将空间问题转化为平面问题的转化思想也是处理空间问题最常用的思路．
练习册系列答案
相关题目
16、如图：已知平面α∥平面β，点A、B在平面α内，点C、D在β内，直线AB与CD是异面直线，点E、F、G、H分别是线段AC、BC、BD、AD的中点，求证：
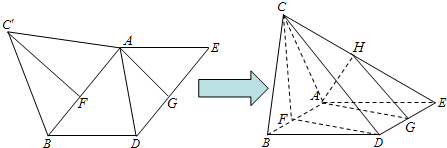
（2013•烟台二模）如图，E是以AB为直径的半圆上异于A、B的点，矩形ABCD所在的平面垂直于该半圆所在的平面，且AB=2AD=2．