题目内容
设一个圆锥的底面半径为r,高为h,母线为l.
(1)若r=2,h=6,求圆锥的侧面积Mc,表面积Mb和体积V;
(2)判断各种不同形状的圆锥,表达式
是否为定值,并说明理由.
(1)若r=2,h=6,求圆锥的侧面积Mc,表面积Mb和体积V;
(2)判断各种不同形状的圆锥,表达式
| (Mb-Mc)Mb(2Mc-Mb) | V2 |
分析:(1)直接利用圆锥的侧面积公式,表面积公式,体积公式求解即可.
(2)利用(1)的公式,代入表达式
化简,结合圆锥的底面半径为r,高为h,母线为l,满足勾股定理,即可推出结果.
(2)利用(1)的公式,代入表达式
| (Mb-Mc)Mb(2Mc-Mb) |
| V2 |
解答:解:(1)依题意得Mc=πrl…①Mb=πrl+πr2…②V=
πr2h…③
∵r=2,h=6,∴l2=r2+h2=22+62=40,∴l=2
.
代入已知条件得Mc=4
π,Mb=4(1+
)π,V=8π.(6分)
(2)证明:由(1)①②③得:
=
(10分)
又因为圆锥的底面半径为r,高为h,母线为l,
∴h2+r2=l2所以
=9π(定值). (12分)
| 1 |
| 3 |
∵r=2,h=6,∴l2=r2+h2=22+62=40,∴l=2
| 10 |
代入已知条件得Mc=4
| 10 |
| 10 |
(2)证明:由(1)①②③得:
| (Mb-Mc)Mb(2Mc-Mb) |
| V2 |
| 9π(l2-r2) |
| h2 |
又因为圆锥的底面半径为r,高为h,母线为l,
∴h2+r2=l2所以
| (Mb-Mc)Mb(2Mc-Mb) |
| V2 |
点评:本题是基础题,考查圆锥的体积,表面积,侧面积的求法,注意圆锥的底面半径,高,母线满足的勾股定理,是解题的关键,考查计算能力.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
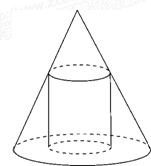 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示. 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.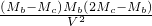 是否为定值,并说明理由.
是否为定值,并说明理由.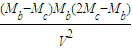 是否为定值,并说明理由.
是否为定值,并说明理由.