题目内容
(2013•闸北区一模)一人在海面某处测得某山顶C的仰角为α(0°<α<45°),在海面上向山顶的方向行进m米后,测得山顶C的仰角为90°-α,则该山的高度为
mtan2α
mtan2α米.(结果化简)
| 1 |
| 2 |
| 1 |
| 2 |
分析:由题可知,在图中直角三角形,在Rt△OBC中,利用α角的正切求出BC;在△ACD中,利用正弦定理,求出山高h.
解答: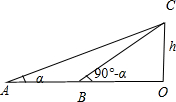 解:令OC=h,在Rt△OBC中,由sin(90°-α)=
解:令OC=h,在Rt△OBC中,由sin(90°-α)=
,得BC=
,
在△ACB中,由正弦定理可知
=
=
,
h=
mtan2α.
即山高为:
mtan2α.
故答案为:
mtan2α.
 解:令OC=h,在Rt△OBC中,由sin(90°-α)=
解:令OC=h,在Rt△OBC中,由sin(90°-α)=| OC |
| BC |
| h |
| sin(90°-α) |
在△ACB中,由正弦定理可知
| AB |
| sin(90°-2α) |
| BC |
| sinα |
| h |
| sinαsin(90°-α) |
h=
| 1 |
| 2 |
即山高为:
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用正弦定理解三角形.

练习册系列答案
相关题目