题目内容
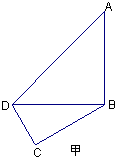
 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点.(1)求证:DC⊥平面ABC;
(2)求BE与平面ABC所成角的正弦值大小.
分析:(1)利用面面垂直证明线面垂直,进而可得线线垂直,再利用∠C=90°,可得DC⊥BC,从而可得线面垂直;
(2)取AC中点F,连接EF、FB,证明EF⊥平面ABC,可得∠EBF为BE与平面ABC所成角,从而可求BE与平面ABC所成角的正弦值大小.
(2)取AC中点F,连接EF、FB,证明EF⊥平面ABC,可得∠EBF为BE与平面ABC所成角,从而可求BE与平面ABC所成角的正弦值大小.
解答:(1)证明:∵∠A=45°,AB=BD,∴∠ABD=90°,∴AB⊥BD
∵平面ABD⊥平面BDC,平面ABD∩平面BDC=BD
∴AB⊥平面BDC,
∵DC?平面BDC,∴AB⊥DC
∵∠C=90°,∴DC⊥BC
∵AB∩BC=B,∴DC⊥平面ABC;
(2)解:取AC中点F,连接EF、FB,则
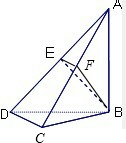
∵点E为棱AD的中点,∴EF∥DC,EF=
DC
∵DC⊥平面ABC
∴EF⊥平面ABC,
∴∠EBF为BE与平面ABC所成角
∵BE=
AB
∴sin∠EBF=
=
=
∴BE与平面ABC所成角的正弦值为
∵平面ABD⊥平面BDC,平面ABD∩平面BDC=BD
∴AB⊥平面BDC,
∵DC?平面BDC,∴AB⊥DC
∵∠C=90°,∴DC⊥BC
∵AB∩BC=B,∴DC⊥平面ABC;
(2)解:取AC中点F,连接EF、FB,则

∵点E为棱AD的中点,∴EF∥DC,EF=
| 1 |
| 2 |
∵DC⊥平面ABC
∴EF⊥平面ABC,
∴∠EBF为BE与平面ABC所成角
∵BE=
| ||
| 2 |
∴sin∠EBF=
| EF |
| BE |
| ||||
|
| ||
| 4 |
∴BE与平面ABC所成角的正弦值为
| ||
| 4 |
点评:本题考查面面垂直的性质,考查线面垂直,考查线面角,正确运用线面垂直的判定,作出线面角是关键.

练习册系列答案
相关题目
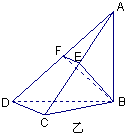
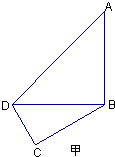 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.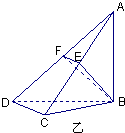
 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.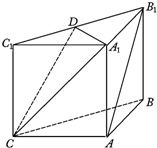 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.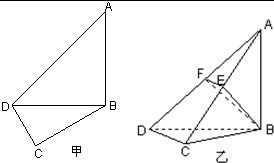 在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.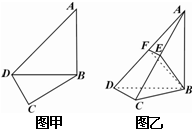 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.