题目内容
若函数
在点
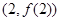处的切线为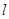
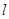，则直线与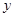
轴的交点坐标为_________.
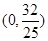
解析试题分析：根据题意，由于函数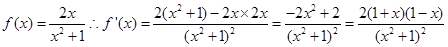
，那么可知当x=2时可知导数值为
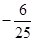，且该点的函数值为
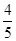，则由点斜式方程可知方程为y-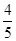=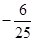(x-2)令x=0,得到y=
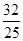,故可知直线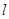与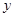轴的交点坐标为。
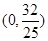考点：导数的几何意义
点评：主要是考查了导数的求解切线方程的运用，属于基础题。
练习册系列答案
相关题目
题目内容
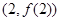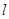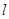若函数在点处的切线为，则直线与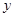轴的交点坐标为_________.
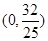
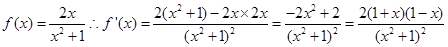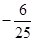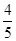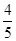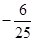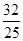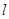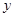解析试题分析：根据题意，由于函数，那么可知当x=2时可知导数值为 ，且该点的函数值为，则由点斜式方程可知方程为y-=(x-2)令x=0,得到y=,故可知直线与轴的交点坐标为。
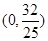考点：导数的几何意义
点评：主要是考查了导数的求解切线方程的运用，属于基础题。
．若曲线
与直线
所围成封闭图形的面积为
,则
______．
在区间
上最大值与最小值的和为 
的导数为 .
的最大值是 
，
都是定义在R上的函数，
，
，
，且
，
，在有穷数列
中，任意取正整数
，则前
项和大于
的概率是 
是曲线
的一条切线，则实数b＝ ___ ．
为抛物线
上两点，点
，过点
，则点
，则函数
图像与直线
围成的封闭图形的面积是__________。