题目内容
已知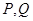 为抛物线
为抛物线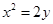 上两点,点
上两点,点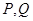 的横坐标分别为
的横坐标分别为 ,过点
,过点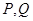 分别作抛物线的切线,两切线交于点
分别作抛物线的切线,两切线交于点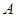 ,则点
,则点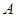 的坐标为
的坐标为
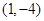
解析试题分析:因为点P,Q的横坐标分别为4,-2,
代入抛物线方程得P,Q的纵坐标分别为8,2.
由x2=2y,则y= x2,所以y′=x,
x2,所以y′=x,
过点P,Q的抛物线的切线的斜率分别为4,-2,
所以过点P,Q的抛物线的切线方程分别为y=4x-8,y=-2x-2
联立方程组解得x=1,y=-4
故点A的纵坐标为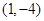 。
。
考点:本题主要考查导数的几何意义,直线方程,直线交点的求法。
点评:中档题,曲线的切线斜率,等于在切点的导函数值。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
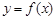 的图象在点
的图象在点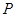 处的切线方程为
处的切线方程为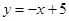 ,则
,则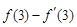 = .
= .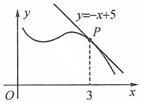
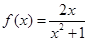 在点
在点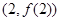 处的切线为
处的切线为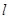 ,则直线
,则直线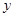 轴的交点坐标为_________.
轴的交点坐标为_________.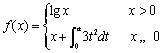 ,若
,若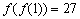 ,则
,则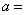 .
.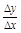 为 .
为 . 与抛物线
与抛物线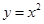 所围成的图形面积是___________________.
所围成的图形面积是___________________.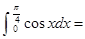
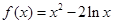 的单调递减区间为________.
的单调递减区间为________.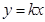 是
是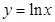 的切线,则
的切线,则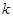 的值为
的值为