题目内容
某地区森林原有木材存量为a,且每年增长率为25%,因生产建设的需要每年年底要砍伐的木材量为b,设an为n年后该地区森林木材的存量.(1)求an的表达式;
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不少于
| 7 |
| 9 |
| 19a |
| 72 |
分析:(1)要求出an的表达式,主要思路是求出前几项然后观察规律,从而推出得出an的表达式,求解即可
(2)只需代入b=
,化简后的指数式转化利用对数的运算即可顺利解答.
(2)只需代入b=
| 19a |
| 72 |
解答:解:(1)设第一年的森林的木材存量为a1,
第n年后的森林的木材存量为an,
则a1=a(1+
)-b=
a-b,a2=
a1-b=(
)2a-(
+1)b,a3=
a2-b=(
)3a-[(
)2+
+1]b,
所以an=(
)na-[(
)n-1+(
)n-2+…+1]=(
)na-4[(
)n-1]b(n∈N*).
(2)当b=
a时,有an<
a得(
)na-4[(
)n-1]×
a<
a即(
)n>5,
所以,n>
=
≈7.2.
答:经过8年后该地区就开始水土流失.
第n年后的森林的木材存量为an,
则a1=a(1+
| 1 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
所以an=(
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
(2)当b=
| 19 |
| 72 |
| 7 |
| 9 |
| 5 |
| 4 |
| 5 |
| 4 |
| 19 |
| 72 |
| 7 |
| 9 |
| 5 |
| 4 |
所以,n>
| lg5 |
| lg5-2lg2 |
| 1-lg2 |
| 1-3lg2 |
答:经过8年后该地区就开始水土流失.
点评:本题的背景较为熟悉,所用的知识是递推数列的概念,函数思想.严格意义上说,由a1,a2,得出an的表达式,需要证明,但此处的应用问题主要是求出即可,证明大可不必.解答(2)直接代入化简即可,要解答(
)n>5,转化为对数的运算是解答本题的关键,两边取常用对数可解答.
| 5 |
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
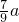 ,如果
,如果 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3) ,如果
,如果 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)