题目内容

设函数f(x)=|x2-4x-5|.

（1）在区间［-2，6］上画出函数f(x)的图象.

（2）设集合A={x|f(x)≥5},B=(-∞,-2］∪［0,4］∪［6,+∞).试判断集合A和B之间的关系，并给出证明.

（3）当k＞2时，求证：在区间［-1，5］上，y=kx+3k的图象位于函数f(x)图象的上方.

（1）解析：

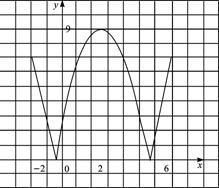
（2）解析：方程f(x)=5的解分别是2-，0，4和2+，由于f(x)在（-∞,-1］和［2，5］上单调递减，在［-1,2］和［5,+∞)上单调递增，因此

A=（-∞,2-］∪［0,4］∪［2+,+∞).

由于2+＜6,2-＞-2,∴BA.

(3)证明:当x∈［-1,5］时，f(x)=-x2+4x+5.

g(x)=k(x+3)-(-x2+4x+5)

=x2+(k-4)x+(3k-5)

=(x-)2-,

∵k＞2,∴＜1.又-1≤x≤5,

①当-1≤＜1,即2＜k≤6时，取x=.

g(x)min=-=-［(k-10)2-64］.

∵16≤(k-10)2＜64,

∴(k-10)2-64＜0,

则g(x)min＞0.

②当＜-1,即k＞6时，取x=-1,g(x)min=2k＞0.

由①、②可知，当k＞2时，g(x)＞0,x∈［-1,5］.

因此，在区间［-1，5］上，y=k(x+3)的图象位于函数f(x)图象的上方.

练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设函数f（x）=p（x-
1
x
）-2lnx，g（x）=
2e
x
（p是实数，e为自然对数的底数）
（1）若f（x）在其定义域内为单调函数，求p的取值范围；
（2）若直线l与函数f（x），g（x）的图象都相切，且与函数f（x）的图象相切于点（1，0），求p的值；
（3）若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求p的取值范围．
设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+1）≥f（x），则称f（x）为M上的高调函数．现给出下列三个命题：
①函数f(x)=(
12
)x为R上的l高调函数；
②函数f（x）=sin2x为R上的π高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围[2，+∞）；
其中正确的命题是
②③
②③
（填序号）
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网