题目内容
关于函数f(x)=2sin(3x- ),有下列命题:
),有下列命题:
①其最小正周期为 ,②其图象由y=2sin3x向左平移
,②其图象由y=2sin3x向左平移 个单位而得到,③在[
个单位而得到,③在[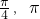 ]上为单调递增函数.
]上为单调递增函数.
则其中真命题为________.
①
分析:由y=Asin(ωx+φ)周期公式,可得①是真命题;根据函数图象平移的公式,可得②所描述的平移不正确;根据函数y=Asin(ωx+φ)的单调区间求法,可得函数不是区间[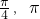 ]上的单调递增函数,故③不正确,由此得到正确答案.
]上的单调递增函数,故③不正确,由此得到正确答案.
解答:对于①,根据函数y=Asin(ωx+φ)周期公式,可得f(x)=2sin(3x- )的最小正周期为T=
)的最小正周期为T= ,故①正确;
,故①正确;
对于②,函数f(x)=2sin(3x- )的图象是由y=2sin3x向右平移
)的图象是由y=2sin3x向右平移 个单位或向左平移
个单位或向左平移 单位而得到,故②不正确;
单位而得到,故②不正确;
对于③,令- +2kπ≤3x-
+2kπ≤3x- ≤
≤ +2kπ,得
+2kπ,得 +
+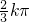 ≤x≤
≤x≤ +
+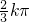 ,(k∈Z)
,(k∈Z)
得函数在[ ,
, ]和[
]和[ ,
,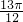 ]上是增函数,而在区间[
]上是增函数,而在区间[ ,
, ]上是减函数,
]上是减函数,
由此可得函数在[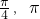 ]上先增后减再增,故③不正确.
]上先增后减再增,故③不正确.
故答案为:①
点评:本题给出一个形如y=Asin(ωx+φ)的函数,要我们求它的周期性和单调性,着重考查了三角函数的图象与性质的知识,属于基础题.
分析:由y=Asin(ωx+φ)周期公式,可得①是真命题;根据函数图象平移的公式,可得②所描述的平移不正确;根据函数y=Asin(ωx+φ)的单调区间求法,可得函数不是区间[
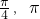 ]上的单调递增函数,故③不正确,由此得到正确答案.
]上的单调递增函数,故③不正确,由此得到正确答案.解答:对于①,根据函数y=Asin(ωx+φ)周期公式,可得f(x)=2sin(3x-
 )的最小正周期为T=
)的最小正周期为T= ,故①正确;
,故①正确;对于②,函数f(x)=2sin(3x-
 )的图象是由y=2sin3x向右平移
)的图象是由y=2sin3x向右平移 个单位或向左平移
个单位或向左平移 单位而得到,故②不正确;
单位而得到,故②不正确;对于③,令-
 +2kπ≤3x-
+2kπ≤3x- ≤
≤ +2kπ,得
+2kπ,得 +
+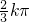 ≤x≤
≤x≤ +
+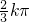 ,(k∈Z)
,(k∈Z)得函数在[
 ,
, ]和[
]和[ ,
,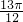 ]上是增函数,而在区间[
]上是增函数,而在区间[ ,
, ]上是减函数,
]上是减函数,由此可得函数在[
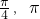 ]上先增后减再增,故③不正确.
]上先增后减再增,故③不正确.故答案为:①
点评:本题给出一个形如y=Asin(ωx+φ)的函数,要我们求它的周期性和单调性,着重考查了三角函数的图象与性质的知识,属于基础题.

练习册系列答案
相关题目