题目内容
已知函数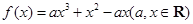 .
.
(1)当 时,求函数
时,求函数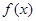 的极值;
的极值;
(2)若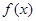 在区间
在区间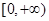 上单调递增,试求
上单调递增,试求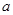 的取值或取值范围
的取值或取值范围
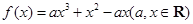 .
.(1)当
 时,求函数
时,求函数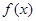 的极值;
的极值;(2)若
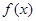 在区间
在区间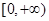 上单调递增,试求
上单调递增,试求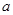 的取值或取值范围
的取值或取值范围(1)极大值为1,极小值为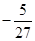 ;(2)
;(2)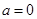 .
.
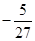 ;(2)
;(2)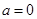 .
.试题分析:(1)当
 时,令导数等于零得极值点,代入函数求得极值;(2)若
时,令导数等于零得极值点,代入函数求得极值;(2)若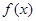 在区间
在区间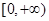 上是单调递增函数,则
上是单调递增函数,则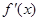 在区间
在区间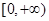 内恒大于或等于零,讨论求得
内恒大于或等于零,讨论求得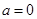 .
.试题解析:(1)当
 时,
时,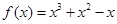 ,∴
,∴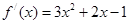 ,
,令
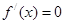 ,则
,则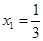 ,
, , 2分
, 2分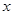 、
、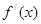 和
和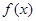 的变化情况如下表
的变化情况如下表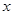 | 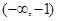 | 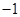 | 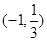 | 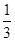 | 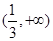 |
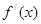 | + | 0 | 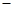 | 0 | + |
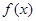 |  | 极大值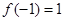 |  | 极小值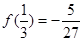 |  |
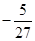 ; 5分
; 5分(2)
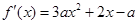 ,
,若
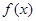 在区间
在区间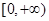 上是单调递增函数, 则
上是单调递增函数, 则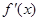 在区间
在区间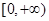 内恒大于或等于零, 6分
内恒大于或等于零, 6分若
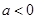 ,这不可能, 7分
,这不可能, 7分若
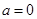 ,则
,则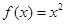 符合条件, 9分
符合条件, 9分若
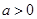 ,则由二次函数
,则由二次函数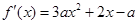 的性质知
的性质知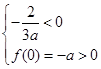 ,即
,即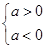 ,这也不可能, 13分
,这也不可能, 13分所以
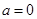 14分
14分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
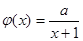 ,
,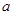 为正常数.
为正常数.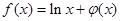 ,且
,且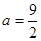 ,求函数
,求函数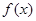 的单调增区间;
的单调增区间;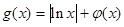 ,且对任意
,且对任意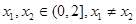 都有
都有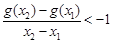 ,求
,求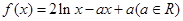 .
.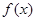 的单调性;
的单调性;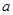 的值,使不等式
的值,使不等式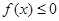 恒成立.
恒成立.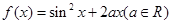 ,若对任意实数
,若对任意实数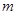 ,直线
,直线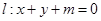 都不是曲线
都不是曲线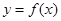 )的切线,则
)的切线,则
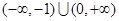

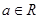 且
且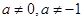
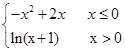 ,若| f(x)|≥ax,则a的取值范围是( )
,若| f(x)|≥ax,则a的取值范围是( )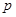 在曲线
在曲线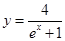 上,
上, 为曲线在点
为曲线在点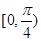
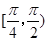
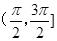

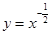 在点
在点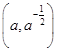 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则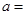 ( )
( )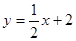 ,则
,则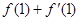 =______
=______