题目内容
用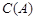 表示非空集合
表示非空集合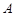 中元素的个数,定义
中元素的个数,定义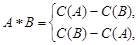
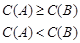 ,若
,若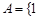 ,
,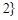 ,
,
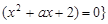 ,且
,且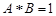 ,设实数
,设实数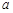 的所有可能取值构成集合
的所有可能取值构成集合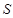 ,则
,则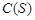 =( )
=( )
A. | B.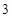 |
C.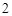 | D. |
B
解析试题分析:由已知得: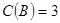 或
或 ,当
,当 时,即
时,即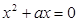 由两个相等实根,
由两个相等实根, 即
即 且
且 没有实根,
没有实根,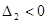 ,即
,即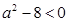 ,
, ,
, ;当
;当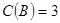 时,即
时,即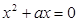 由两个相等实根,
由两个相等实根, 即
即 且
且 由两个不等实根,
由两个不等实根,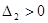 ,
, ,
, 或
或 ,不成立,当
,不成立,当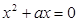 由两个不等实根,
由两个不等实根, 即
即 且
且 由两个相等实根,
由两个相等实根,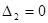 ,
, ,
,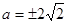 ,
, ,所以
,所以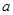 有3个值,即选B.
有3个值,即选B.
考点:1.二次方程根的个数;2.集合元素.

练习册系列答案
相关题目
记集合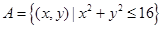 和集合
和集合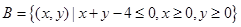 表示的平面区域分别为
表示的平面区域分别为 ,若在区域
,若在区域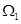 内任取一点
内任取一点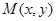 ,则点M落在区域
,则点M落在区域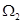 的概率为( )
的概率为( )
A.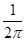 | B. | C.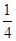 | D.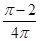 |
已知集合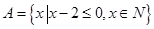 ,
,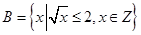 ,则满足条件
,则满足条件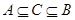 的集合
的集合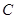 的个数为( )
的个数为( )
A.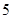 | B.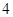 | C.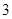 | D.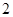 |
设全集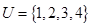 ,集合
,集合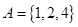 ,
,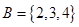 ,则
,则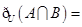 ( )
( )
A.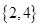 | B.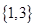 | C.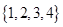 | D.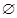 |
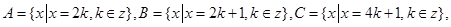 又
又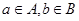 则( )
则( )
A.a+b A A | B.a+b B B |
C.a+b C C | D.a+b A,B,C中的任一个 A,B,C中的任一个 |
集合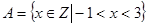 的元素个数是 ( )
的元素个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
A={x|x≠1,x∈R}∪{y|y≠2,y∈R},B={z|z≠1且z≠2,z∈R},那么( )
| A.A=B | B.A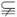 B B |
C.B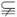 A A | D.A∩B=? |