题目内容
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为 .
.(Ⅰ)求p的值;
(Ⅱ)若直角三角形ABC的三个顶点在抛物线L上,且直角顶点B的横坐标为1,过点A、C分别作抛物线L的切线,两切线相交于点D,直线AC与y轴交于点E,当直线BC的斜率在[3,4]上变化时,直线DE斜率是否存在最大值,若存在,求其最大值和直线BC的方程;若不存在,请说明理由.

【答案】分析:(Ⅰ)联立方程组,利用弦长公式,直接求出p的值;
(Ⅱ)设A(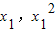 ),C(
),C(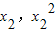 ),设BC的斜率为k,
),设BC的斜率为k, ,求出kAC,得到直线AC的方程,求出ED的斜率,利用函数的单调性求出斜率AD的最大值,求出BC的方程.
,求出kAC,得到直线AC的方程,求出ED的斜率,利用函数的单调性求出斜率AD的最大值,求出BC的方程.
解答:(Ⅰ) 解:由 解得A(0,0),B(2p,2p)…2分
解得A(0,0),B(2p,2p)…2分
∴ =AB=
=AB= ,
,
∴p= …5分
…5分
(Ⅱ) 解:B(1,1),设A( ),C(
),C(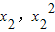 ),
), =x1+x2,
=x1+x2,
设BC的斜率为k,则 ⇒x2-kx+k-1=0,
⇒x2-kx+k-1=0,
△=k2-4k+4≥0,
又1+x2=k⇒x2=k-1,C(k-1,(k-1)2), ,
,
kAC=x1+x2=k-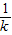 -2,
-2,
直线AC的方程为y-(k-1)2=(k- -2)[x-(k-1)],
-2)[x-(k-1)],
令x=0,y=k- ,所以E(0,k-
,所以E(0,k- ),
),
AD:y- =2x1(x-x1)⇒y=2x1x-
=2x1(x-x1)⇒y=2x1x- ,
,
同理CD:y=2x2x-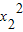 ,
,
联立两方程得D( (k-
(k- -2),
-2), ),
),
kED= =
= =
=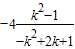 =-4
=-4 ,
,
令u= -k,在[3,4]递减,所以,当k=4时,kED最大为
-k,在[3,4]递减,所以,当k=4时,kED最大为 ,
,
所以,BC的方程为y-1=4(x-1)即4x-y-3=0…12分
点评:本题是中档题,考查直线与圆锥曲线方程的综合问题,设而不求的思想,韦达定理的应用,函数的单调性等知识,考查计算能力转化思想的应用.
(Ⅱ)设A(
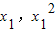 ),C(
),C(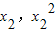 ),设BC的斜率为k,
),设BC的斜率为k, ,求出kAC,得到直线AC的方程,求出ED的斜率,利用函数的单调性求出斜率AD的最大值,求出BC的方程.
,求出kAC,得到直线AC的方程,求出ED的斜率,利用函数的单调性求出斜率AD的最大值,求出BC的方程.解答:(Ⅰ) 解:由
 解得A(0,0),B(2p,2p)…2分
解得A(0,0),B(2p,2p)…2分∴
 =AB=
=AB= ,
,∴p=
 …5分
…5分(Ⅱ) 解:B(1,1),设A(
 ),C(
),C(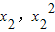 ),
), =x1+x2,
=x1+x2,设BC的斜率为k,则
 ⇒x2-kx+k-1=0,
⇒x2-kx+k-1=0,△=k2-4k+4≥0,
又1+x2=k⇒x2=k-1,C(k-1,(k-1)2),
 ,
,kAC=x1+x2=k-
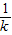 -2,
-2,直线AC的方程为y-(k-1)2=(k-
 -2)[x-(k-1)],
-2)[x-(k-1)],令x=0,y=k-
 ,所以E(0,k-
,所以E(0,k- ),
),AD:y-
 =2x1(x-x1)⇒y=2x1x-
=2x1(x-x1)⇒y=2x1x- ,
,同理CD:y=2x2x-
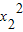 ,
,联立两方程得D(
 (k-
(k- -2),
-2), ),
),kED=
 =
= =
=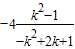 =-4
=-4 ,
,令u=
 -k,在[3,4]递减,所以,当k=4时,kED最大为
-k,在[3,4]递减,所以,当k=4时,kED最大为 ,
,所以,BC的方程为y-1=4(x-1)即4x-y-3=0…12分
点评:本题是中档题,考查直线与圆锥曲线方程的综合问题,设而不求的思想,韦达定理的应用,函数的单调性等知识,考查计算能力转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
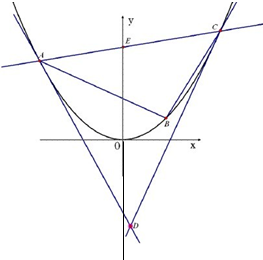 已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为 .
.
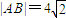 .
.