题目内容
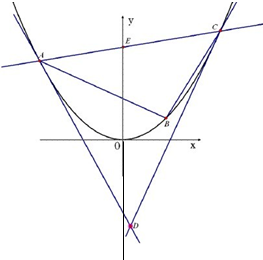
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦|AB|=4| 2 |
(1)求p的值;
(2)抛物线L上是否存在异于点A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.若存在,求出点C的坐标;若不存在,请说明理由.
分析:(1)把直线方程与抛物线方程联立,求出A与B的坐标,再代入弦长即可求p的值;
(2)设出点C的坐标以及圆的圆心N,利用A、B、C三点在圆上,得出圆心坐标N和点C的坐标之间的关系式;再利用抛物线L在点C处的切线与NC垂直,代入即可求点C的坐标.
(2)设出点C的坐标以及圆的圆心N,利用A、B、C三点在圆上,得出圆心坐标N和点C的坐标之间的关系式;再利用抛物线L在点C处的切线与NC垂直,代入即可求点C的坐标.
解答:解:(1)由
解得A(0,0),B(2p,2p)
∴4
=AB=
=2
p,
∴p=2
(2)由(1)得x2=4y,A(0,0),B(4,4)
假设抛物线L上存在异于点A、B的点C(t,
)(t≠0,t≠4),使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线
令圆的圆心为N(a,b),
则由
得
得
?
∵抛物线L在点C处的切线斜率k=y′|x=t=
(t≠0)
又该切线与NC垂直,
∴
•
=-1?2a+bt-2t-
t3=0
∴2•(-
)+t•
-2t-
t3=0?t3-2t2-8t=0
∵t≠0,t≠4,
∴t=-2
故存在点C且坐标为(-2,1).
|
∴4
| 2 |
| 4p2+4p2 |
| 2 |
∴p=2
(2)由(1)得x2=4y,A(0,0),B(4,4)
假设抛物线L上存在异于点A、B的点C(t,
| t2 |
| 4 |
令圆的圆心为N(a,b),
则由
|
|
得
|
|
∵抛物线L在点C处的切线斜率k=y′|x=t=
| t |
| 2 |
又该切线与NC垂直,
∴
b-
| ||
| a-t |
| t |
| 2 |
| 1 |
| 4 |
∴2•(-
| t2+4t |
| 8 |
| t2+4t+32 |
| 8 |
| 1 |
| 4 |
∵t≠0,t≠4,
∴t=-2
故存在点C且坐标为(-2,1).
点评:本题主要考查直线上两点的斜率公式、直线与圆相切、垂径定理、抛物线与圆的几何性质等知识,考查学生的基本思想与运算能力、探究能力和推理能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为 .
.
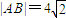 .
.