题目内容
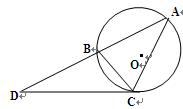
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆O于点E、F,点M在EF上,且 :
:
(I)求证:PA·PB=PM·PQ.
(II)求证: .
.
(I) 见解析;(II) 见解析.
解析试题分析:(I)证明A,Q,M,B四点共圆,可得结论; (II)先证明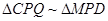 ,再证明
,再证明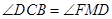 ,可得
,可得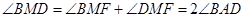 ,
,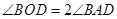 ,所以
,所以 .
.
试题解析:(Ⅰ)∵∠BAD=∠BMF,所以A,Q,M,B四点共圆, 3分
所以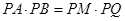 . 5分
. 5分
(Ⅱ)∵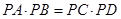 , ∴
, ∴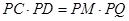 ,
,
又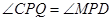 , 所以
, 所以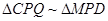 , 7分
, 7分
∴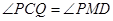 ,则
,则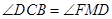 , 8分
, 8分
∵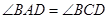 ,∴
,∴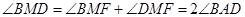 ,
,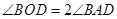 ,所以
,所以 . 10分
. 10分
考点:1、几何证明.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 内接于
内接于 上,
上, ,
, 交
交 于点E,点F在DA的延长线上,
于点E,点F在DA的延长线上, ,求证:
,求证:
 是
是 .
.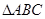 中,
中,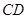 是
是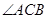 的角平分线,
的角平分线, 的外接圆交
的外接圆交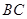 于
于 ,
,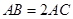 .
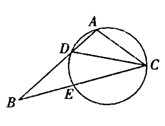
.
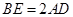 ;
;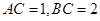 时,求
时,求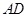 的长.
的长.
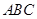 内接于⊙
内接于⊙ ,
, ,直线
,直线 切⊙
切⊙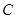 ,弦
,弦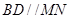 ,
, 相交于点
相交于点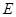 .
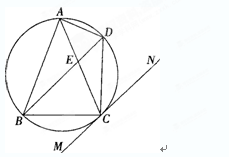
.
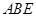 ≌△
≌△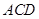 ;
;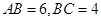 ,求
,求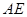 长.
长.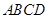 的外接圆为⊙
的外接圆为⊙ ,
,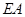 是⊙
是⊙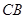 的延长线与
的延长线与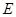 ,
,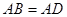 .
.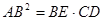 .
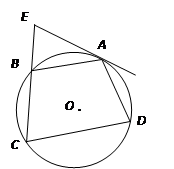
.
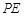 切⊙
切⊙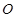 于点E,割线PBA交⊙
于点E,割线PBA交⊙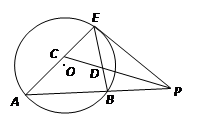
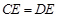 ;
;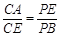 .
.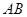 是圆
是圆 的直径,
的直径,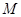 为圆上一点,
为圆上一点, ,垂足为
,垂足为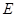 ,点
,点 为圆
为圆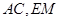 交于点
交于点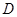 ,
,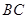 交
交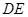 于点
于点 .
.
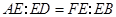 ;(2)
;(2)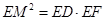 .
.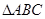 的外接圆,过点C的圆的切线与AB的延长线交于点D,
的外接圆,过点C的圆的切线与AB的延长线交于点D,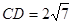 ,AB=BC=3,求BD以及AC的长.
,AB=BC=3,求BD以及AC的长.