题目内容
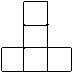
用若干块相同的小正方体搭成一个几何体,该几何几的三视图如下图所示,则搭成该几何体需要的小正方体的块数是 ( )
| A.8 | B.7 | C.6 | D.5 |
C
解析考点:由三视图求面积、体积.
分析:结合三视图,画出几何体的直观图,即可判断搭成该几何体最少需要的小正方体的块数.
解:由题意可知,
三视图复原几何体是下层四个小正方体,
上层一个正方体,如图,
搭成该几何体最少需要的小正方体的块数:6.
故选C.
点评:本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.

练习册系列答案
相关题目
已知球的体积与其表面积的数值相等,则此球的半径为( )
| A.4 | B.3 | C.2 | D.1 |
若某几何体的三视图(单位:cm)如图所示,则几何体的体积为
A.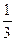 cm cm | B.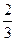 cm cm | C.1cm | D.2cm |
球内接正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则这个正方体的表面积与正四面体的表面积之比是
A. | B.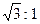 | C. | D.2:  |
一个与球心距离为1的平面截球所得圆面面积为 ,则球的表面积为( )
,则球的表面积为( )
A. | B. |
C. | D. |