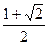题目内容
在△ABC中,AB=2,BC=1.5,∠ABC=120o,若使绕直线BC旋转一周,则所形成的几何体的体积是
A. | B. | C. | D. |
D
解析考点:棱柱、棱锥、棱台的体积;旋转体(圆柱、圆锥、圆台).
专题:计算题.
分析:所形成的几何体是以ACD为轴截面的圆锥中挖去了一个以ABD为轴截面的小圆锥后剩余的部分,故用大圆锥的体积减去小圆锥的体积,即为所求.
解答:解:如图: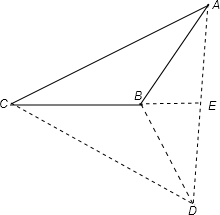
△ABC中,绕直线BC旋转一周,
则所形成的几何体是以ACD为轴截面的圆锥中挖去了一个以ABD为轴截面的小圆锥后剩余的部分.
∵AB=2,BC=1.5,∠ABC=120°,∴AE=ABsin60°= 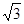 ,BE=ABcos60°=1,
,BE=ABcos60°=1,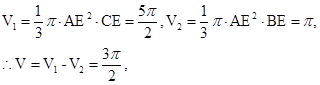
故选D.

练习册系列答案
相关题目
用若干块相同的小正方体搭成一个几何体,该几何几的三视图如下图所示,则搭成该几何体需要的小正方体的块数是 ( )
| A.8 | B.7 | C.6 | D.5 |
若一个三角形采用斜二测画法作出其直观图,则其直观图的面积是原来三角形面积的( )
A. 倍 倍 | B. 倍 倍 | C. 倍 倍 | D. 倍 倍 |
一空间几何体按比例绘制的三视图如图所示(单位:m) 
则该几何体的体积(单位:m3)为 ( )
A. | B. | C. | D. |

 .
.





 的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,B与D两点之间的球面距离为
的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,B与D两点之间的球面距离为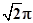



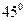 ,腰和上底均为
,腰和上底均为 的等腰梯形,那么原平面图形的面积是( )
的等腰梯形,那么原平面图形的面积是( )