题目内容
设函数f(x)=(x-2)2+blnx,其中b为常数.(Ⅰ)若函数f(x)在定义域上单调递增,求b的取值范围;
(Ⅱ)若b≤0,求函数f(x)的极值点;
(Ⅲ)当b=-6时,利用函数f(x)的性质证明:对任意大于1的正整数n,不等式
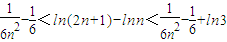 恒成立.
恒成立.
【答案】分析:(1)先由负数没有对数得到f(x)的定义域,求出f(x)的导函数,根据b大于 2得到导函数大于0,所以函数在定义域内单调递增;
(2)令f(x)的导函数等于0,求出此时方程的解即可得到x的值,根据d小于等于0舍去不在定义域范围中的解,得到符合定义域的解,然后利用这个解把(0,+∞)分成两段,讨论导函数的正负得到函数f(x)的增减性,根据f(x)的增减性即可得到函数的唯一极小值为这个解;
(3)由b=-6,代入f(x)的解析式中确定出f(x),并根据(2)把b的值代入求出的唯一极小值中求出值为 3,得到函数的递减区间为(0,3),根据当n>1时,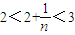 ,利用函数为减函数恒有
,利用函数为减函数恒有 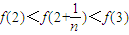 ,化简得证.
,化简得证.
解答:解:(1)由题意知,f(x)的定义域为(0,+∞),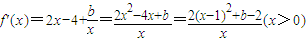 .
.
∴当 b>2时,f′(x)>0,函数f(x)在定义域(0,+∞)上单调递增;
(2)令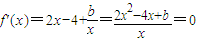 ,
,
得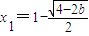 ,
, .
.
当b≤0时,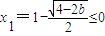 ∉(0,+∞)(舍去),
∉(0,+∞)(舍去),
而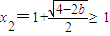 ∈(0,+∞),
∈(0,+∞),
此时:f′(x),f(x)随x在定义域上的变化情况如下表:
由此表可知:∵b≤0时,f(x)有惟一极小值点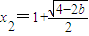 ;
;
(3)由(2)可知当b=-6时,函数f(x)=(x-2)2-6lnx,此时f(x)有惟一极小值点:x=3,
且 x∈(0,3)时,f′(x)<0,f(x)在(0,3)为减函数.
∵当n>1时,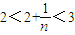 ,
,
∴恒有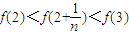 ,
,
∴当n>1时,恒有不等式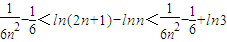 成立.
成立.
点评:此题考查学生会利用导函数的正负判断函数的单调性,并根据函数的单调性得到函数的极值,掌握导数在最值问题中的应用,是一道综合题.学生做题时应注意找出函数的定义域.第三问的突破点是令b=-6,然后利用增减性进行证明.
(2)令f(x)的导函数等于0,求出此时方程的解即可得到x的值,根据d小于等于0舍去不在定义域范围中的解,得到符合定义域的解,然后利用这个解把(0,+∞)分成两段,讨论导函数的正负得到函数f(x)的增减性,根据f(x)的增减性即可得到函数的唯一极小值为这个解;
(3)由b=-6,代入f(x)的解析式中确定出f(x),并根据(2)把b的值代入求出的唯一极小值中求出值为 3,得到函数的递减区间为(0,3),根据当n>1时,
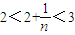 ,利用函数为减函数恒有
,利用函数为减函数恒有 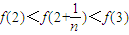 ,化简得证.
,化简得证.解答:解:(1)由题意知,f(x)的定义域为(0,+∞),
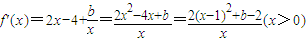 .
.∴当 b>2时,f′(x)>0,函数f(x)在定义域(0,+∞)上单调递增;
(2)令
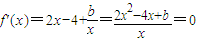 ,
,得
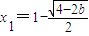 ,
, .
. 当b≤0时,
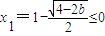 ∉(0,+∞)(舍去),
∉(0,+∞)(舍去),而
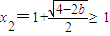 ∈(0,+∞),
∈(0,+∞),此时:f′(x),f(x)随x在定义域上的变化情况如下表:

由此表可知:∵b≤0时,f(x)有惟一极小值点
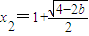 ;
;(3)由(2)可知当b=-6时,函数f(x)=(x-2)2-6lnx,此时f(x)有惟一极小值点:x=3,
且 x∈(0,3)时,f′(x)<0,f(x)在(0,3)为减函数.
∵当n>1时,
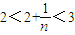 ,
,∴恒有
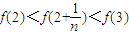 ,
,∴当n>1时,恒有不等式
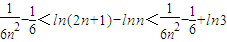 成立.
成立.点评:此题考查学生会利用导函数的正负判断函数的单调性,并根据函数的单调性得到函数的极值,掌握导数在最值问题中的应用,是一道综合题.学生做题时应注意找出函数的定义域.第三问的突破点是令b=-6,然后利用增减性进行证明.

练习册系列答案
相关题目
 的最小值;
的最小值; 的最小值;
的最小值;