题目内容
设函数f(x)=x(x-1)2,x>0.(1)求f(x)的极值;
(2)设0<a≤1,记f(x)在(0,a]上的最大值为F(a),求函数
 的最小值;
的最小值;(3)设函数g(x)=lnx-2x2+4x+t(t为常数),若使g(x)≤x+m≤f(x)在(0,+∞)上恒成立的实数m有且只有一个,求实数m和t的值.
【答案】分析:(1)求导,令f′(x)=0得x= 或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.
或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.
(2)由(1)知f(x)的单调性,以极值点为界,把a分成两类讨论,在两类分别求出F(a),求G(a),求G(a)最小值,两个最小值最小者,即为所求.
(3)把连等式分成两个不等式x+m-g(x)≥0和f(x)-x-m≥0在(0,+∞)上恒成立的问题,把不等式的左边看作一个函数,利用导数求最小值,两个范围求交集再由实数m有且只有一个,可求m,进而求t.
解答:解:(1)f′(x)=(x-1)2+2x(x-1)=3x2-4x+1=(3x-1)(x-1),x>0.令f′(x)=0,得x= 或x=1,f(x),f′(x)随x的变化情况如下表
或x=1,f(x),f′(x)随x的变化情况如下表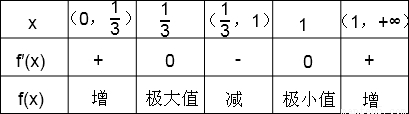
∴当x= 时,有极大值f(
时,有极大值f( )=
)=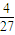 ,当x=1时,有极小值f(1)=0.
,当x=1时,有极小值f(1)=0.
(2)由(1)知:f(x)在(0, ],[1,+∞)上是增函数,在[
],[1,+∞)上是增函数,在[ ,1]上是减函数,
,1]上是减函数,
①0<a≤ 时,F(a)=a(a-1)2,G(a)=(a-1)2≥
时,F(a)=a(a-1)2,G(a)=(a-1)2≥
特别的,当a= 时,有G(a)=
时,有G(a)= ,
,
②当 <a≤1时,F(a)=f(
<a≤1时,F(a)=f( )=
)=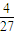 ,G(a)=
,G(a)=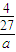 ≥
≥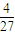
特别的,当a=1时,有G(a)=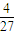 ,
,
由①②知,当0<a≤1时,函数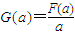 的最小值为
的最小值为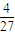 .
.
(3)由已知得h1(x)=x+m-g(x)=2x2-3x-lnx+m-t≥0在(0,+∞)上恒成立,
∵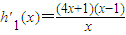 ,
,
∴x∈(0,1)时,h′1(x)<0,x∈(1,+∞)时,h1(x)>0
∴x=1时,h′1(x)取极小值,也是最小值,
∴当h1(1)=m-t-1≥0,m≥t+1时,h1(x)≥0在(0,+∞)上恒成立,
同样,h2(x)=f(x)-x-m=x3-2x2-m≥0在(0,+∞)上恒成立,
∵h′2(x)=3x(x- ),
),
∴x∈(0, )时,h′2(x)<0,x∈(
)时,h′2(x)<0,x∈( ,+∞),h′2(x)>0,
,+∞),h′2(x)>0,
∴x= 时,h2(x)取极小值,也是最小值,
时,h2(x)取极小值,也是最小值,
∴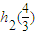 =-
=-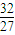 -m≥0,m≤-
-m≥0,m≤-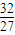 时,h2(x)≥0在(0,+∞)上恒成立,
时,h2(x)≥0在(0,+∞)上恒成立,
∴t+1≤m≤-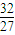 ,
,
∵实数m有且只有一个,∴m=-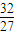 ,t=
,t=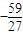 .
.
点评:本题了考查导数与极值的关系,若f(a)=0:a的左侧f'(x)>0,a的右侧f'(x)<0则a是极大值点;a的左侧f'(x)<0,a的右侧f'(x)>0则a是极小值点;求F(a)时,要分类讨论,在求参数的范围时,经过两次转化为求函数的最值,使问题得以解决.
 或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.
或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.(2)由(1)知f(x)的单调性,以极值点为界,把a分成两类讨论,在两类分别求出F(a),求G(a),求G(a)最小值,两个最小值最小者,即为所求.
(3)把连等式分成两个不等式x+m-g(x)≥0和f(x)-x-m≥0在(0,+∞)上恒成立的问题,把不等式的左边看作一个函数,利用导数求最小值,两个范围求交集再由实数m有且只有一个,可求m,进而求t.
解答:解:(1)f′(x)=(x-1)2+2x(x-1)=3x2-4x+1=(3x-1)(x-1),x>0.令f′(x)=0,得x=
 或x=1,f(x),f′(x)随x的变化情况如下表
或x=1,f(x),f′(x)随x的变化情况如下表
∴当x=
 时,有极大值f(
时,有极大值f( )=
)=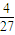 ,当x=1时,有极小值f(1)=0.
,当x=1时,有极小值f(1)=0.(2)由(1)知:f(x)在(0,
 ],[1,+∞)上是增函数,在[
],[1,+∞)上是增函数,在[ ,1]上是减函数,
,1]上是减函数,①0<a≤
 时,F(a)=a(a-1)2,G(a)=(a-1)2≥
时,F(a)=a(a-1)2,G(a)=(a-1)2≥
特别的,当a=
 时,有G(a)=
时,有G(a)= ,
,②当
 <a≤1时,F(a)=f(
<a≤1时,F(a)=f( )=
)=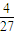 ,G(a)=
,G(a)=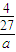 ≥
≥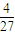
特别的,当a=1时,有G(a)=
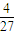 ,
,由①②知,当0<a≤1时,函数
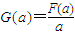 的最小值为
的最小值为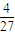 .
.(3)由已知得h1(x)=x+m-g(x)=2x2-3x-lnx+m-t≥0在(0,+∞)上恒成立,
∵
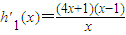 ,
,∴x∈(0,1)时,h′1(x)<0,x∈(1,+∞)时,h1(x)>0
∴x=1时,h′1(x)取极小值,也是最小值,
∴当h1(1)=m-t-1≥0,m≥t+1时,h1(x)≥0在(0,+∞)上恒成立,
同样,h2(x)=f(x)-x-m=x3-2x2-m≥0在(0,+∞)上恒成立,
∵h′2(x)=3x(x-
 ),
),∴x∈(0,
 )时,h′2(x)<0,x∈(
)时,h′2(x)<0,x∈( ,+∞),h′2(x)>0,
,+∞),h′2(x)>0,∴x=
 时,h2(x)取极小值,也是最小值,
时,h2(x)取极小值,也是最小值,∴
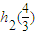 =-
=-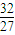 -m≥0,m≤-
-m≥0,m≤-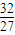 时,h2(x)≥0在(0,+∞)上恒成立,
时,h2(x)≥0在(0,+∞)上恒成立,∴t+1≤m≤-
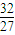 ,
,∵实数m有且只有一个,∴m=-
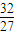 ,t=
,t=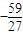 .
.点评:本题了考查导数与极值的关系,若f(a)=0:a的左侧f'(x)>0,a的右侧f'(x)<0则a是极大值点;a的左侧f'(x)<0,a的右侧f'(x)>0则a是极小值点;求F(a)时,要分类讨论,在求参数的范围时,经过两次转化为求函数的最值,使问题得以解决.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|