题目内容
下列命题中,正确的命题有 ( )
①用相关系数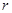 来判断两个变量的相关性时,
来判断两个变量的相关性时,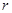 越接近0,说明两个变量有较强的相关性;
越接近0,说明两个变量有较强的相关性;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量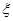 服从正态分布N(0,1),若
服从正态分布N(0,1),若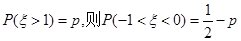 ;
;
④回归直线一定过样本点的中心
①用相关系数
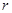 来判断两个变量的相关性时,
来判断两个变量的相关性时,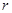 越接近0,说明两个变量有较强的相关性;
越接近0,说明两个变量有较强的相关性;②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量
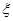 服从正态分布N(0,1),若
服从正态分布N(0,1),若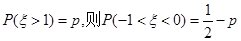 ;
;④回归直线一定过样本点的中心

| A.1个 | B.2个 | C.3个 | D.4个 |
C
试题分析:命题1中,用相关系数
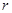 来判断两个变量的相关性时,那么只有r的绝对值越趋近于0,那么说明相关性越弱,r的绝对值越趋近于1,则说明相关性越强,故错误。
来判断两个变量的相关性时,那么只有r的绝对值越趋近于0,那么说明相关性越弱,r的绝对值越趋近于1,则说明相关性越强,故错误。命题2中,根据方差的性质,对于一组数据加上一个常数后其方差不变,成立
命题3中,由于随机变量的正态分布值标准正太分布,期望值为0,方差为1,那么根据正态分布图像,可知其图像的对称轴为y轴,因此由P(
 )=p,那么可知P(
)=p,那么可知P(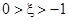 )=
)=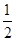 (1-2 P(
(1-2 P( ))=
))=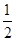 (1-2p)=
(1-2p)=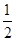 -p,故成立。
-p,故成立。命题4中那么利用回归直线y=bx+a,且
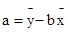 ,那么两式联立得到
,那么两式联立得到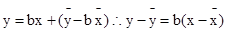 则其一定过样本点的中心
则其一定过样本点的中心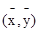 ,故成立,选C
,故成立,选C点评:解决该试题的关键是理解相关系数r对于相关性的影响,以及方差表示的为数据的稳定性,以及正态分布中,概率值的求解要利用对称性来得到。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
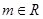 ,命题
,命题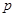 :对任意
:对任意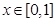 ,不等式
,不等式 恒成立;命题
恒成立;命题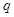 :存在
:存在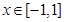 ,使得
,使得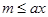 成立
成立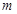 的取值范围;
的取值范围;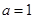 ,若
,若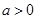 且
且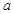 的取值范围。
的取值范围。 :所有有理数都是实数;命题
:所有有理数都是实数;命题 :正数的对数都是负数,则下列命题中为真命题的是( )
:正数的对数都是负数,则下列命题中为真命题的是( )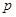 :
: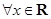 ,
,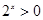 ,那么命题
,那么命题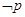 为( )
为( )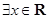 ,
,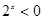
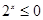
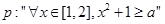 命题
命题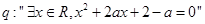 ,当命题
,当命题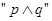 是真命题,则实数a的取值范围是 ( )
是真命题,则实数a的取值范围是 ( ) 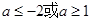
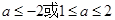
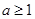
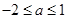
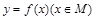 是奇函数”的否定是( )
是奇函数”的否定是( )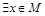 ,
,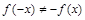
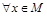 ,
, 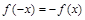
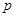 :关于
:关于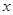 的不等式
的不等式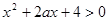 ,对一切
,对一切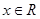 恒成立,命题
恒成立,命题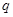 :函数
:函数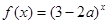 是增函数,若
是增函数,若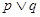 为真,
为真,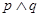 为假,求实数
为假,求实数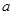 的取值范围.
的取值范围.