题目内容
已知下列命题:①已知p、q为两个命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题;
②已知随机变量X服从正态分布N(3,1),且P(2≤x≤4)=0.6826,则P(x>4)=0.1587;
③“
 ”是“一元二次方程x2+x+m=0有实根”的必要不充分条件;
”是“一元二次方程x2+x+m=0有实根”的必要不充分条件;④命题“若a>b,则2a>2b-1”的否命题为:若a≤b,则2a≤2b-1.
其中不正确的命题个数为( )
A.0
B.1
C.2
D.3
【答案】分析:根据复合命题真假的规则判断出①正确;根据正态分布的概率规则判断出②正确;根据二次方程有实根的充要条件判断出③不正确;根据四种命题的形式判断出④正确.
解答:解:对于①,因为“p∨q”为假命题,所以命题p,q都是假命题,所以¬p,¬q都是真命题,所以“¬p∧¬q”为真命题,故①正确;
对于②,因为P(2≤x≤4)=0.6826,所以P(3≤x≤4)=0.3413,所以P(x>4)=0.5-0.3413=0.1587,故②正确;
对于③,因为“一元二次方程x2+x+m=0有实根”充要条件是△=1-4m≥0即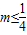 ,
,
因为“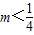 ”能推出“
”能推出“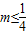 ,”成立,反之推不出,所以“
,”成立,反之推不出,所以“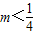 ”是“一元二次方程x2+x+m=0有实根”的充分不必要条件,故③错;
”是“一元二次方程x2+x+m=0有实根”的充分不必要条件,故③错;
对于④,若a>b,则2a>2b-1”的否命题为:若a≤b,则2a≤2b-1,所以④正确;
故答案为B.
点评:本题考查复合命题的真值表、四种命题的形式及有关充要条件的定义,属于一道基础题.
解答:解:对于①,因为“p∨q”为假命题,所以命题p,q都是假命题,所以¬p,¬q都是真命题,所以“¬p∧¬q”为真命题,故①正确;
对于②,因为P(2≤x≤4)=0.6826,所以P(3≤x≤4)=0.3413,所以P(x>4)=0.5-0.3413=0.1587,故②正确;
对于③,因为“一元二次方程x2+x+m=0有实根”充要条件是△=1-4m≥0即
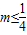 ,
,因为“
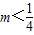 ”能推出“
”能推出“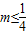 ,”成立,反之推不出,所以“
,”成立,反之推不出,所以“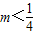 ”是“一元二次方程x2+x+m=0有实根”的充分不必要条件,故③错;
”是“一元二次方程x2+x+m=0有实根”的充分不必要条件,故③错;对于④,若a>b,则2a>2b-1”的否命题为:若a≤b,则2a≤2b-1,所以④正确;
故答案为B.
点评:本题考查复合命题的真值表、四种命题的形式及有关充要条件的定义,属于一道基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目