题目内容

（2012•福建）在△ABC中，已知∠BAC=60°，∠ABC=45°，BC=
3
，则AC=
2
2
．
分析：结合已知两角一对边，要求B的对边，可利用正弦定理，
AC
sinB
=
BC
sinA
进行求解
解答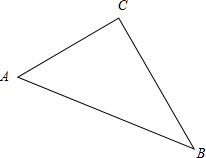：解：∵∠BAC=60°，∠ABC=45°，
∴BC=
3

由正弦定理可得，
AC
sinB
=
BC
sinA
可得AC=
BCsinB
sinA
=
3
×sin45°
sin60°
=
2

故答案为：
2
点评：本题主要考查了正弦定理在解三角形中的应用，掌握正弦定理及其使用的范围是求解的关键
练习册系列答案
相关题目
（2012•福建）已知关于x的不等式x2-ax+2a＞0在R上恒成立，则实数a的取值范围是
（0，8）
（0，8）
．
（2012•福建）已知函数f（x）=ex+ax2-ex，a∈R．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求函数f（x）的单调区间；
（Ⅱ）试确定a的取值范围，使得曲线y=f（x）上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．
（2012•福建模拟）在直角梯形ABCD中，AD∥BC，BC=2AD=2AB=2
2
，∠ABC=90°，如图1．把△ABD沿BD翻折，使得平面ABD⊥平面BCD，如图2．
（Ⅰ）求证：CD⊥AB；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离；
（Ⅲ）在线段BC上是否存在点N，使得AN与平面ACD所成角为60°？若存在，求出
BN
BC
的值；若不存在，说明理由．
（2012•福建）在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．
（Ⅰ）求an和bn；
（Ⅱ）现分别从{an}和{bn}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网