题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,向量 =(1,λsinA),
=(1,λsinA), =(sinA,1+cosA),且
=(sinA,1+cosA),且 ∥
∥
(Ⅰ)若λ=2,求角A的大小;
(Ⅱ)若sinB+sinC= sinA,求实数λ的取值范围.
sinA,求实数λ的取值范围.
解:(Ⅰ)由 ∥
∥ ,得2sin2A-1-cosA=0,化为2cos2A+cosA-1=0,
,得2sin2A-1-cosA=0,化为2cos2A+cosA-1=0,
解得cosA= 或cosA=-1(舍去),
或cosA=-1(舍去),
∴A= .
.
(Ⅱ)∵sinB+sinC= sinA,
sinA,
由正弦定理得b+c= a,
a,
由 ∥
∥ ,得λsin2A-1-cosA=0,化为λcos2A+cosA+1-λ=0,
,得λsin2A-1-cosA=0,化为λcos2A+cosA+1-λ=0,
解得cosA=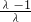 或cosA=-1(舍去).
或cosA=-1(舍去).
又cosA= =
=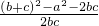 =
=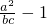
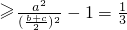 ,
,
综上,λ需要满足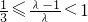 ,解得λ≥
,解得λ≥ .
.
分析:(Ⅰ)利用向量共线的充要条件即可得出;
(Ⅱ)利用正弦、余弦定理及基本不等式即可得出.
点评:熟练掌握向量共线的充要条件、正弦、余弦定理、基本不等式及不等式的解法是解题的关键.
 ∥
∥ ,得2sin2A-1-cosA=0,化为2cos2A+cosA-1=0,
,得2sin2A-1-cosA=0,化为2cos2A+cosA-1=0,解得cosA=
 或cosA=-1(舍去),
或cosA=-1(舍去),∴A=
 .
.(Ⅱ)∵sinB+sinC=
 sinA,
sinA,由正弦定理得b+c=
 a,
a,由
 ∥
∥ ,得λsin2A-1-cosA=0,化为λcos2A+cosA+1-λ=0,
,得λsin2A-1-cosA=0,化为λcos2A+cosA+1-λ=0,解得cosA=
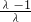 或cosA=-1(舍去).
或cosA=-1(舍去).又cosA=
 =
=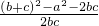 =
=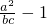
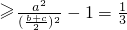 ,
,综上,λ需要满足
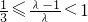 ,解得λ≥
,解得λ≥ .
.分析:(Ⅰ)利用向量共线的充要条件即可得出;
(Ⅱ)利用正弦、余弦定理及基本不等式即可得出.
点评:熟练掌握向量共线的充要条件、正弦、余弦定理、基本不等式及不等式的解法是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |